 por jones_slash » Seg Jun 07, 2010 22:49
por jones_slash » Seg Jun 07, 2010 22:49
Como posso mostrar q 13 elevado a 3n + 17 elevado a 3n é múltiplo
de 45 para todo n E N ímpar??
-
jones_slash
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Sáb Jun 05, 2010 17:05
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: tecnico em eletrotecnica e eletronica
- Andamento: formado
 por davi_11 » Ter Jun 08, 2010 14:22
por davi_11 » Ter Jun 08, 2010 14:22
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
 por davi_11 » Qui Jun 10, 2010 14:12
por davi_11 » Qui Jun 10, 2010 14:12
Cometi um equivoco na ultima linha e peço mil desculpas, na verdade confundi as propriedades.
Talvez de para se provar usando indução sobre n.
"Se é proibido pisar na grama, o jeito é deitar e rolar..."
-
davi_11
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 02, 2010 22:47
- Localização: Leme - SP
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: Curso técnico em eletrotécnica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



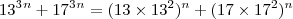
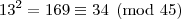


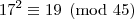
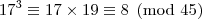
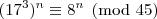
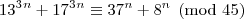
 divide 45, então
divide 45, então  também divide.
também divide.



 .
.



