 por hevhoram » Qua Jun 02, 2010 11:50
por hevhoram » Qua Jun 02, 2010 11:50
ola amigos nao consegui fazer esta questao de razão se alguem souber me responder fico feliz tow enviando apergunta com a resposta e como eu estava procedendo
20 – Um funcionário desconta do seu salário bruto 1/4 para o Imposto de renda e 1/8 para sua associação. Calcule a razão entre os descontos e o salário líquido.
R: 3/5
4/4 – 1/4 = 3/4 então 4/4 / 3/4 = 16/12
8/8 – 1/8 = 7/8 então 8/8 / 7/8 = 64/56 daí não sei como proceder
-

hevhoram
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qua Jun 02, 2010 11:43
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: informática educacional
- Andamento: formado
 por Molina » Qua Jun 02, 2010 18:43
por Molina » Qua Jun 02, 2010 18:43
Boa tarde.
Chamaremos o salário do funcionário de x.
Sendo assim, seus descontos são:

e

Somando os
descontos:
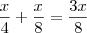
Ou seja, seu
líquido é de
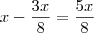
Fazendo a razão que se pede:
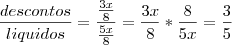
Bom estudo!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- razao
por hevhoram » Qua Jun 02, 2010 20:14
- 2 Respostas
- 1677 Exibições
- Última mensagem por hevhoram

Qui Jun 03, 2010 20:42
Álgebra Elementar
-
- Razão
por Guaciara » Qui Set 23, 2010 22:40
- 2 Respostas
- 2406 Exibições
- Última mensagem por Guaciara

Qui Set 23, 2010 23:31
Conversão de Unidades
-
- razão
por angeloka » Sex Out 15, 2010 19:29
- 8 Respostas
- 6792 Exibições
- Última mensagem por MarceloFantini

Sáb Out 23, 2010 01:41
Álgebra Elementar
-
- PA com razão 0,3
por gustavowelp » Sex Nov 19, 2010 08:42
- 5 Respostas
- 3443 Exibições
- Última mensagem por 0 kelvin

Sex Nov 19, 2010 15:51
Progressões
-
- Razão 17
por Raphael Feitas10 » Qui Fev 17, 2011 01:22
- 1 Respostas
- 1495 Exibições
- Última mensagem por DanielFerreira

Qui Fev 17, 2011 17:24
Funções
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 e
e 
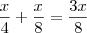
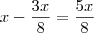
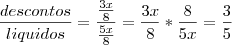



 .
.



