 por RJ1572 » Dom Abr 04, 2010 13:22
por RJ1572 » Dom Abr 04, 2010 13:22
1 - Carlos comprou um objeto e revendeu por R$171,00, ganhando nesta transação tantos por cento quanto o preço de compra. Qual o preço de compra?
A resposta segundo o gabarito é R$90,00 mas não consigo chegar a este resultado..Alguém pode me ajudar na resolução?
Obrigado.
-
RJ1572
- Usuário Dedicado

-
- Mensagens: 36
- Registrado em: Sex Fev 26, 2010 13:00
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por estudandoMat » Dom Abr 04, 2010 17:26
por estudandoMat » Dom Abr 04, 2010 17:26
Valor = x
Venda = 171
tantos por cento quanto o preço de compra, ou seja, o valor da compra é igual o valor da % colocada no preço.
Monta uma formula:
x + x.

= 171
Resolvendo
x² + 100x - 17100 = 0

x =
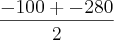
x' =
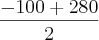
= 90 (serve, pois 90 + 90% de 90 = 171)
x" =
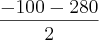
= -190 (não serve)
-
estudandoMat
- Usuário Parceiro

-
- Mensagens: 52
- Registrado em: Sex Abr 02, 2010 00:29
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema - Lógica
por RJ1572 » Seg Mar 01, 2010 13:08
- 1 Respostas
- 1572 Exibições
- Última mensagem por DanielFerreira

Qua Mar 03, 2010 08:28
Álgebra Elementar
-
- Problema lógica
por RJ1572 » Dom Abr 04, 2010 21:32
- 1 Respostas
- 1462 Exibições
- Última mensagem por estudandoMat

Seg Abr 05, 2010 00:05
Álgebra Elementar
-
- problema de lógica
por Gladimir » Ter Fev 04, 2014 17:18
- 1 Respostas
- 1377 Exibições
- Última mensagem por fff

Ter Fev 04, 2014 17:40
Lógica
-
- Problema de Logica + conjunto.
 por Aninha Mendes » Seg Fev 13, 2012 17:43
por Aninha Mendes » Seg Fev 13, 2012 17:43
- 1 Respostas
- 2500 Exibições
- Última mensagem por LuizAquino

Seg Fev 13, 2012 22:09
Conjuntos
-
- Problema usando a lógica
por virginia » Sáb Abr 27, 2013 11:52
- 1 Respostas
- 1565 Exibições
- Última mensagem por Jhennyfer

Sáb Abr 27, 2013 17:22
Lógica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 = 171
= 171
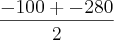
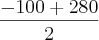 = 90 (serve, pois 90 + 90% de 90 = 171)
= 90 (serve, pois 90 + 90% de 90 = 171)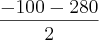 = -190 (não serve)
= -190 (não serve)


 , avisa que eu resolvo.
, avisa que eu resolvo.

