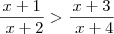
O que fiz foi, passa o 2º termo p/ o primeiro, ficaria:
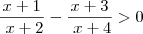
depois, mmc;

Depois eu não sei o que fazer. Sei que o resultado esperado é {-4<x<-2}. Se alguém puder me dar uma ajuda eu agradeço.







Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.