Karina escreveu:Uma editora pretende despachar um lote de livros, agrupados em 100 pacotes de
20 cm X 20 cm X 30 cm. A transportadora acondicionará esses pacotes em caixas com formato de bloco retangular de
40 cm X 40 cm X 60 cm. A quantidade minima necessária de caixas para esse envio é:
a) 9
b) 11
c) 13
d) 15
e) 17
Alguem pode me ajudar? Eu não consigui interpretar direito
esse problema, não sei por onde começar
Boa tarde, Karina.
Vou tentar te ajudara interpretar o problema, e não resolvê-lo:
Temos aqui um problema envolvendo volumes. Chamaremos de
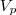
o volume total do pacote e de

o volume total da caixa. Tanto os pacotes, quanto a caixa são paralelepípedos. A fórmula para o volume deste sólido é dado por

, onde a, b e c são os lados do paralelepípedo.
Então comece fazendo isso, verificando o volume de um pacote e o volume de uma caixa. Agora que você tem a informação do volume do pacote, lembre-se que iremos despachar 100 pacotes. Então basta fazer

. Com isso você vai descobrir o
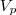
que é o volume total dos pacotes.
Como queremos saber quantas caixas são necessárias para armazenas esses pacotes, basta dividir os volumes:
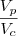
.
Você chegará num valor 'não-inteiro'. Logo, o menor número de caixas necessárias é o menor inteiro maior do que este 'não-inteiro'.
Acho que com isso você consegue resolver.
Aguardo sua confirmação.



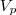 o volume total do pacote e de
o volume total do pacote e de  o volume total da caixa. Tanto os pacotes, quanto a caixa são paralelepípedos. A fórmula para o volume deste sólido é dado por
o volume total da caixa. Tanto os pacotes, quanto a caixa são paralelepípedos. A fórmula para o volume deste sólido é dado por  , onde a, b e c são os lados do paralelepípedo.
, onde a, b e c são os lados do paralelepípedo. . Com isso você vai descobrir o
. Com isso você vai descobrir o 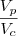 .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.