O valor da prestação do apartamento de paulo corresponde a quarta parte do seu salário.
As despesas com alimentação, saúde, transporte, e lazer correspondem a dois quintos do seu salário.
Paulo deseja economizar, mensalmente, no minimo 420 reais. Sendo assim quanto deve ser, no minimo, o salário de Paulo
a) 840 reais
b) 935 reais
c) 12060 reais
d) 930 reais
e) 1200 reais
Não consigo resolver este problema, alguem pode ajudar?


 o salário, temos:
o salário, temos: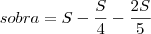
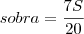
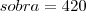 (pelo menos)
(pelo menos)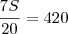

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)