Flavio Cacequi escreveu:Sabe-se que x - 1/x =V5. Calcule o valor de x^6 - 1/x^6.
a)135V5
b)125V5
c)144V5
d)36V5
e)18V5
Bem, confesso que não consigui fazer essa questão do jeito mais apropriado (manipulando a expressão), mas como ninguem respondeu vou colocar a forma que eu utilizei pra chegar na resposta, letra c.
Antes, só por teimosia minha, não é um sinal de + ao inves do - na expressão x^6 - 1/x^6 ? Se fosse um + a questão seria bem mais simples.
Vamos então pra forma que eu utilizei.
1) Descobrir o valor de "x".
Multiplicando toda expressão ( x - 1/x = V5 ) por "x"
![\\
x*(x-1/x)=x*\left(\sqrt[2]{5} \right)\\
\\
x^2-1=\sqrt[2]{5}x\\
\\
x^2-\sqrt[2]{5}x-1=0\\
\\ \\
x*(x-1/x)=x*\left(\sqrt[2]{5} \right)\\
\\
x^2-1=\sqrt[2]{5}x\\
\\
x^2-\sqrt[2]{5}x-1=0\\
\\](/latexrender/pictures/0195fe3929618c65cbde616dabfad76e.png)
Resolvendo por Bhaskara
![\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{\left(\sqrt[2]{5} \right)^2-4*1*-1}}{2*1}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{5+4}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{9}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm3}{2} \\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{\left(\sqrt[2]{5} \right)^2-4*1*-1}}{2*1}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{5+4}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{9}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm3}{2}](/latexrender/pictures/9376215df8abaacf97b8acd6517f7aa4.png)
Agora que vem a parte menos elegante da resolução. Escolhendo uma das raizes (pode ser qlq uma das duas, so muda o sinal no final), vamos achar a expressão pedida no braço. Como as raizes achadas estão separadas em dois termos devido a presença da raiz quadrada a conta fica muito extensa, logo vamos achar uma aproximação para
![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png)
.
Por tentativa não é dificil achar que
![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png)
é aproximadamente 2.23, logo

.
Agora achamos a expressão de
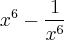
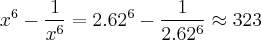
Esse é o resultado utilizando a aproximação que fizemos, no entanto a questão da as respostas em termos de
![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png)
.
Pra resolver esse problema, basta dividirmos a resposta encontrada por
![\sqrt[2]{5}\approx2.23 \sqrt[2]{5}\approx2.23](/latexrender/pictures/7f5cb7c8761e7bbdae0026f59e0dd57f.png)
![323=323*\frac{\sqrt[2]{5}}{2.23}=\frac{323}{2.23}*\sqrt[2]{5}\approx144.84\sqrt[2]{5} 323=323*\frac{\sqrt[2]{5}}{2.23}=\frac{323}{2.23}*\sqrt[2]{5}\approx144.84\sqrt[2]{5}](/latexrender/pictures/80bf018481617943b367e3a952b2629b.png)
Espero que tenha ajudado, bons estudos.



![\\
x*(x-1/x)=x*\left(\sqrt[2]{5} \right)\\
\\
x^2-1=\sqrt[2]{5}x\\
\\
x^2-\sqrt[2]{5}x-1=0\\
\\ \\
x*(x-1/x)=x*\left(\sqrt[2]{5} \right)\\
\\
x^2-1=\sqrt[2]{5}x\\
\\
x^2-\sqrt[2]{5}x-1=0\\
\\](/latexrender/pictures/0195fe3929618c65cbde616dabfad76e.png)
![\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{\left(\sqrt[2]{5} \right)^2-4*1*-1}}{2*1}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{5+4}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{9}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm3}{2} \\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{\left(\sqrt[2]{5} \right)^2-4*1*-1}}{2*1}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{5+4}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm\sqrt[2]{9}}{2}\\
\\
x=\frac{\sqrt[2]{5}\pm3}{2}](/latexrender/pictures/9376215df8abaacf97b8acd6517f7aa4.png)
![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png) .
.![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png) é aproximadamente 2.23, logo
é aproximadamente 2.23, logo  .
. 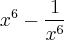
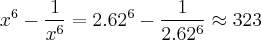
![\sqrt[2]{5} \sqrt[2]{5}](/latexrender/pictures/28fccd6e3bab3b28511a875ab32e94c3.png) .
.![\sqrt[2]{5}\approx2.23 \sqrt[2]{5}\approx2.23](/latexrender/pictures/7f5cb7c8761e7bbdae0026f59e0dd57f.png)
![323=323*\frac{\sqrt[2]{5}}{2.23}=\frac{323}{2.23}*\sqrt[2]{5}\approx144.84\sqrt[2]{5} 323=323*\frac{\sqrt[2]{5}}{2.23}=\frac{323}{2.23}*\sqrt[2]{5}\approx144.84\sqrt[2]{5}](/latexrender/pictures/80bf018481617943b367e3a952b2629b.png)
