
Ariel, neste caso você poderia resolver de duas formas. O correto é eliminar-se os parênteses primeiro e como não é possível eliminar o parênteses somando os valores que estão dentro dele por causa do "x" e multiplicar pela fração que está do lado de fora, podemos aplicar a distributividade, que é uma das propriedades da aritmética.
Um exemplo de distributividade é:
a(b + c), onde a está multiplicando pela soma de b com c, assim:
a(b + c) = ab + ac
Um exemplo com números seria:
2(3 + 5) = 2 x 3 + 2 x 5 = 6 + 10 = 16, mas como podemos eliminar os parênteses somando-se primeiramente os números, poderíamos também resolver da seguinte forma:
2(3 + 5) = 2 x 8 = 16, que dá o mesmo resultado.
No caso do problema em questão, teríamos:
PRIMEIRA FORMA DE RESOLUÇÃO:

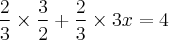
Na multiplicação de frações, multiplica-se o numerador pelo outro numerador e o denominador pelo outro denominador, lembrando que o denominador de 3x é 1, ou seja:
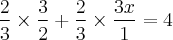
Logo:
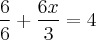
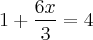

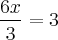
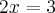
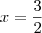

Uma outra forma de se resolver é perceber que existe um número multiplicando pela soma de outro número. Se fôssemos pensar em quadradinhos teríamos algo assim:

e como o primeiro quadradinho está multiplicando, podemos "passar para o outro lado do igual" dividindo, ou seja:

Assim,
SEGUNDA FORMA DE RESOLUÇÃO:


Reescrevendo a fração do lado direito do igual temos:

Uma fração divida pela outra pode ser reescrita em formato de multiplicação da seguinte forma: (Este é apenas um exemplo)

Repare que invertemos o denominador. Usando esta propriedade das frações, podemos continuar resolvendo da seguinte maneira:



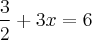
Reorganizando a equação, tem-se que:
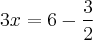
Reescrevendo o 6 como fração temos:

O Mínimo Múltiplo Comum (MMC) de 1 e 2 é 2 (Ver abaixo):
1 - 2 | 2
1 - 1 |
para obter o MMC, basta ir dividindo cada número por um número maior que 1 e ir deixando os resultados do lado esquerdo. Caso a divisão somente seja possível para um deles, divida ele pelo número colocado do lado direito da barra e coloque o resultado embaixo e reptia aquele que não poderá ser dividido.
Exemplo de MMC entre 8 e 15
8 - 15 | 2 (Dá para dividir o 8 por 2 que dá 4 e repete-se o 15 pois ele não pode ser dividido exatamente por 2)
4 - 15 | 2 (Novamente dá para dividir por 2 e repetindo-se o processo acima)
2 - 15 | 2
1 - 15 | 3 (15 pode ser dividido por 3 e como atingirmos 1 do lado esquerdo, paramos por aí mesmo)
1 - 5 | 5 (Cinco somente pode ser dividido por 5, então...)
1 - 1 | - Acabou!
Agora multipliquemos 2 x 2 x 2 x 3 x 5 = MMC = 120
Voltando ao nosso problema e sabendo-se agora que o MMC é 2, deixamos o 2 que é o MMC no denominador. Depois dividimos o MMC pelo denominador de cada fração e multiplicamos pelo numerador, sempre respeitando os sinais:


O passo acima normalmente não é mostrado. Só coloquei para você entender que peguei o MMC = 2, dividi por cada um dos denominadores e multipliquei pelo numerador.
Assim, teremos:
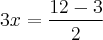
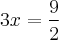
Agora, passando o 3 de 3x dividindo:

e reescrevendo em formato de fração para ficar mais fácil o entendimento:
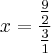
Este formato já vimos anteriormente nesta resolução e portanto, vamos apenas reescrever a fração em formato de multiplicação:
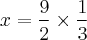
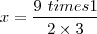

Dá para perceber que 9 e 6 são ambos divisíveis por 3. Então, para simplificar, teremos que dividir OS DOIS (o numerador e o denominador) por 3, ficando com:


Repare que o resultado é o mesmo que obtemos na primeira forma de se resolver o problema. Tivemos mais trabalho nesta segunda, porém é uma forma válida também.
Para saber se o resultado que obtivemos está correto, basta trocar o valor de "x" por este valor encontrado para ver se a igualdade é verdadeira, desta maneira:

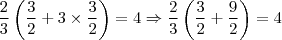
![\Rightarrow \frac{2}{3} \times \frac{12}{2} = 4 \Rightarrow \frac{24}{6} = 4 \;\;\; [Verdadeira] \Rightarrow \frac{2}{3} \times \frac{12}{2} = 4 \Rightarrow \frac{24}{6} = 4 \;\;\; [Verdadeira]](/latexrender/pictures/18f27afc3e19479e60b645e0227c4875.png)
E assim temos a certeza absoluta de que este resultado está correto!
Espero ter ajudado.
Grato
Sandro H. Nakaguma
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali






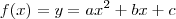 onde para cada valor de x, existe um valor de y (ou f(x)) associado.
onde para cada valor de x, existe um valor de y (ou f(x)) associado.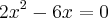


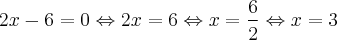
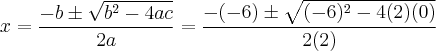
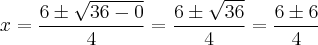
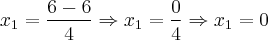
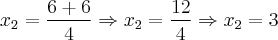

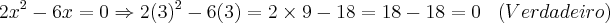
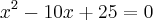









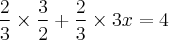
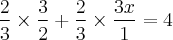
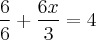
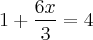

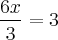
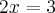
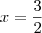










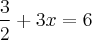
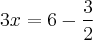



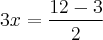
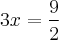

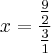
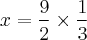
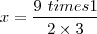




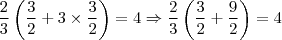
![\Rightarrow \frac{2}{3} \times \frac{12}{2} = 4 \Rightarrow \frac{24}{6} = 4 \;\;\; [Verdadeira] \Rightarrow \frac{2}{3} \times \frac{12}{2} = 4 \Rightarrow \frac{24}{6} = 4 \;\;\; [Verdadeira]](/latexrender/pictures/18f27afc3e19479e60b645e0227c4875.png)


 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
