Houve um erro: Em vez de:
Como p > 0, a terceira condição já é satisfeita. Como p tem que ser maior que p/2 (segunda condição) e também ser maior do que p, então concluimos que x > p.
Sendo assim, x possui somente um único valor positivo pois p é positivo e a resposta é a letra (a)
LEIA-SE:
Como p > 0, a terceira condição já é satisfeita. Como x tem que ser maior que p/2 (segunda condição) e também ser maior do que p, então concluimos que x > p (porque o maior valor entre p/2 e p é ser maior que o próprio p). Lembre-se: x tem que ser maior do que p/2 E x tem que ser maior que p (ao mesmo tempo), ou seja, temos uma interseção:

Sendo assim, x possui somente um único valor positivo pois p é positivo (primeira condição) e deverá ser maior que p, e a resposta é a letra (a).Explicação:p tem que ser positivo (terceira condição). Sabemos que x tem que ser maior que p. Se você escolher um valor para p, existirá um valor para x tal que x seja maior que p de forma que o resultado das somas da equação dada resulte num total de ZERO (0). Por isto, dizemos que existe somente um valor para x, mas ele tem que obedecer as regras encontradas, ou seja, p tem que ser maior que zero, x > p/2, mas como x tem que ser também maior que p, então concluímos que x tem que ser maior que p (pela interseção dos resultados).

Isso para todo p > 0.
Exemplo:
Vamos dar um valor para p que seja maior que zero, por exemplo p = 4. Então:
![\sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0 \Rightarrow \sqrt[]{x-4} - 2 + \sqrt[]{2x-4} = 0 \Rightarrow \sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0 \Rightarrow \sqrt[]{x-4} - 2 + \sqrt[]{2x-4} = 0 \Rightarrow](/latexrender/pictures/239d4363ff71f51a2ec2a722c0b0f97e.png)
![\Rightarrow \sqrt[]{x-4} + \sqrt[]{2x-4} = 2 \Rightarrow \Rightarrow \sqrt[]{x-4} + \sqrt[]{2x-4} = 2 \Rightarrow](/latexrender/pictures/11658441af827fff285a5833c56da3c3.png)
Elevando-se ao quadrado os dois lados da equação, tem-se que:
![\Rightarrow x - 4 + 2\sqrt[]{(x-4)(2x-4)} + 2x - 4 = 4 \Rightarrow 3x - 8 + 2\sqrt[]{2x^2 - 4x - 8x + 16} = 4 \Rightarrow \Rightarrow x - 4 + 2\sqrt[]{(x-4)(2x-4)} + 2x - 4 = 4 \Rightarrow 3x - 8 + 2\sqrt[]{2x^2 - 4x - 8x + 16} = 4 \Rightarrow](/latexrender/pictures/3ed7fc8d31908e5ca02ae69f1e43af87.png)
![\Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 8 - 3x + 4 \Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 12 - 3x \Rightarrow \Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 8 - 3x + 4 \Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 12 - 3x \Rightarrow](/latexrender/pictures/fd304ff36a58cdfe46c55dbe624a0d9f.png)
Elevando-se ao quadrado novamente, ambos os lados da equação final acima, teremos:


Para agilizar, resolendo esta equação quadrática teremos os seguintes valores para x:
![x =4 (3 - \sqrt[]{14}) = -2,97... x =4 (3 - \sqrt[]{14}) = -2,97...](/latexrender/pictures/da55136cd3b82df4e22229d9ba5e051d.png)
![x =4 (3 + \sqrt[]{14}) = 26,97... x =4 (3 + \sqrt[]{14}) = 26,97...](/latexrender/pictures/bf4e35528fe8e483809a96197de29941.png)
Sabemos que se x for negativo, a equação não será válida no conjunto dos números Reais. Assim, x deverá ter o valor 26,97... para que a equação
![\sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0 \sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0](/latexrender/pictures/e2a481733f92f1437c770fb49bfae03b.png)
resulte em zero, como esperado. Como vê, nenhum outro valor de x vai satisfazer a equação para que resulte num total de zero para um valor de p = 4. Assim, para cada valor de p escolhido, existirá um, e somente um valor de x > p > 0 que satisfaça a equação dada no enunciado.
Eu faço a diferença. E você?
Do Poema: Quanto os professores "fazem"?
De Taylor Mali
![\sqrt[]{x-p} - \sqrt[]{p} + \sqrt[]{2x-p} = 0 \sqrt[]{x-p} - \sqrt[]{p} + \sqrt[]{2x-p} = 0](/latexrender/pictures/6c732797890827c23f8958d089bd8681.png) na variável x.
na variável x.

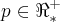
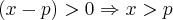
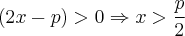
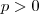




![\sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0 \Rightarrow \sqrt[]{x-4} - 2 + \sqrt[]{2x-4} = 0 \Rightarrow \sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0 \Rightarrow \sqrt[]{x-4} - 2 + \sqrt[]{2x-4} = 0 \Rightarrow](/latexrender/pictures/239d4363ff71f51a2ec2a722c0b0f97e.png)
![\Rightarrow \sqrt[]{x-4} + \sqrt[]{2x-4} = 2 \Rightarrow \Rightarrow \sqrt[]{x-4} + \sqrt[]{2x-4} = 2 \Rightarrow](/latexrender/pictures/11658441af827fff285a5833c56da3c3.png)
![\Rightarrow x - 4 + 2\sqrt[]{(x-4)(2x-4)} + 2x - 4 = 4 \Rightarrow 3x - 8 + 2\sqrt[]{2x^2 - 4x - 8x + 16} = 4 \Rightarrow \Rightarrow x - 4 + 2\sqrt[]{(x-4)(2x-4)} + 2x - 4 = 4 \Rightarrow 3x - 8 + 2\sqrt[]{2x^2 - 4x - 8x + 16} = 4 \Rightarrow](/latexrender/pictures/3ed7fc8d31908e5ca02ae69f1e43af87.png)
![\Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 8 - 3x + 4 \Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 12 - 3x \Rightarrow \Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 8 - 3x + 4 \Rightarrow 2\sqrt[]{2x^2 - 12x + 16} = 12 - 3x \Rightarrow](/latexrender/pictures/fd304ff36a58cdfe46c55dbe624a0d9f.png)


![x =4 (3 - \sqrt[]{14}) = -2,97... x =4 (3 - \sqrt[]{14}) = -2,97...](/latexrender/pictures/da55136cd3b82df4e22229d9ba5e051d.png)
![x =4 (3 + \sqrt[]{14}) = 26,97... x =4 (3 + \sqrt[]{14}) = 26,97...](/latexrender/pictures/bf4e35528fe8e483809a96197de29941.png)
![\sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0 \sqrt[]{x-4} - \sqrt[]{4} + \sqrt[]{2x-4} = 0](/latexrender/pictures/e2a481733f92f1437c770fb49bfae03b.png)


 , avisa que eu resolvo.
, avisa que eu resolvo.

