 por rcpn » Ter Jul 07, 2015 11:09
por rcpn » Ter Jul 07, 2015 11:09
Se a divisão ( x³ - 6x² + 12x - 8)16 + 2x² - 8x + 1 + K / x² - 4x + 4 é exata, o valor de K é:
OBS: a primeira equação entre parêntese está elevado a 16, somado com o restante e dividido pela terceira equação.
Nessa questão, parece se tratar de produto notável, mas mesmo assim eu tive dúvidas em resolver. Se alguém puder me ajudar, agradeço desde já.
-
rcpn
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Ter Abr 08, 2014 10:46
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: formação geral
- Andamento: formado
 por DanielFerreira » Ter Jul 07, 2015 21:25
por DanielFerreira » Ter Jul 07, 2015 21:25
Olá
rcpn, boa noite!
Se a divisão é exata, então podes igualar o divisor (denominador) a zero e substituir o valor encontrado de x no dividendo (numerador).
Consideremos
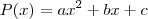
e
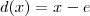
. Se a divisão entre P(x) e d(x) for exata fazemos
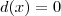
, veja:
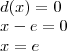
Temos que
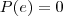
, portanto:
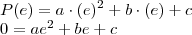
Aplique o raciocínio análogo ao descrito acima e terá a resposta, mas se não conseguir retorne com a dúvida, ok?!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


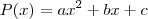 e
e 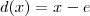 . Se a divisão entre P(x) e d(x) for exata fazemos
. Se a divisão entre P(x) e d(x) for exata fazemos 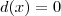 , veja:
, veja: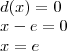
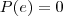 , portanto:
, portanto: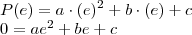



 , avisa que eu resolvo.
, avisa que eu resolvo.

