 por Adrielly » Qui Fev 11, 2010 11:26
por Adrielly » Qui Fev 11, 2010 11:26
Bom, estou estudando para o vestibular! E me deparei com a seuite questão quanto é
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png)
não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é

como isso??
-
Adrielly
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 11, 2010 11:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Fev 11, 2010 12:10
por Molina » Qui Fev 11, 2010 12:10
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Adrielly » Qui Fev 11, 2010 13:41
por Adrielly » Qui Fev 11, 2010 13:41
eu consegui entender até a parte de fatorar o 10, mas e o 2 elevado a 30? como que ele se transformou nesse 1+2² ?
-
Adrielly
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Fev 11, 2010 11:04
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Molina » Qui Fev 11, 2010 14:00
por Molina » Qui Fev 11, 2010 14:00
Ok, vamos lá:
Fazendo a distributiva em
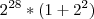
no encontramos

, pois
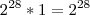
e

Então o que eu fiz foi a operação contrária da distributiva, ou seja, fatorei os termos e coloquei o

em evidência.
Então eu tenho que
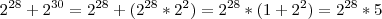
O

continua ali, so que ele está numa forma fatorada. É a mesma coisa que eu escrever
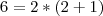
. Caso não tenha ficado claro, informe!

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por rojantsch » Sex Fev 19, 2010 12:56
por rojantsch » Sex Fev 19, 2010 12:56
como se resolve potencias que envolvam frações? so to querendo uma ajuda por favor?
eu preciso fazer um exercicio.
-
rojantsch
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Fev 19, 2010 12:49
- Formação Escolar: ENSINO FUNDAMENTAL II
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Entender o resultado de uma análise de coorelação
por Roniberto » Qua Mai 13, 2009 16:30
- 0 Respostas
- 948 Exibições
- Última mensagem por Roniberto

Qua Mai 13, 2009 16:30
Estatística
-
- Preciso de ajuda com esse exercício
por Dankaerte » Qui Set 10, 2009 19:10
- 2 Respostas
- 6294 Exibições
- Última mensagem por Elcioschin

Ter Abr 13, 2010 14:01
Matrizes e Determinantes
-
- [Integrais] Preciso de ajuda com esse cálculo...
por phvicari » Sáb Set 03, 2011 04:40
- 3 Respostas
- 1872 Exibições
- Última mensagem por LuizAquino

Dom Set 04, 2011 13:30
Cálculo: Limites, Derivadas e Integrais
-
- Preciso saber a fórmula para resolver esse exercício
por Dankaerte » Qui Ago 27, 2009 14:19
- 1 Respostas
- 6967 Exibições
- Última mensagem por Molina

Qui Ago 27, 2009 14:58
Geometria Plana
-
- Como aprender e entender matemática
por Bielto » Sáb Jul 14, 2012 13:55
- 8 Respostas
- 5707 Exibições
- Última mensagem por LuizAquino

Dom Jul 15, 2012 13:18
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png) não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é
não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é  como isso??
como isso??
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png) não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é
não consegui resolver.. tentei tudo que é propriedade de potencia, radiciação..mas nada deu certe, fui olhar no gabarito e vi que a resposta é  como isso??
como isso??
![\sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}} \sqrt[3]{\frac{{2}^{28}+{2}^{30}}{10}}](/latexrender/pictures/b709a448b39c7dc6872fb04edbc002f2.png)
![\sqrt[3]{\frac{{2}^{28}(1+{2}^{2})}{2*5}} \sqrt[3]{\frac{{2}^{28}(1+{2}^{2})}{2*5}}](/latexrender/pictures/c83447ebace86cc855540102cbc53ed7.png)
![\sqrt[3]{\frac{{2}^{28}*5}{2*5}} \sqrt[3]{\frac{{2}^{28}*5}{2*5}}](/latexrender/pictures/2c926a1b36a9536d64f26372fba82eeb.png)
![\sqrt[3]{{2^{27}}} \sqrt[3]{{2^{27}}}](/latexrender/pictures/1091c23a1b9db3cddfb26957cefc8126.png)
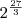




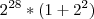 no encontramos
no encontramos  , pois
, pois 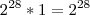 e
e 
 em evidência.
em evidência.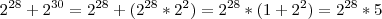
 continua ali, so que ele está numa forma fatorada. É a mesma coisa que eu escrever
continua ali, so que ele está numa forma fatorada. É a mesma coisa que eu escrever 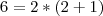 . Caso não tenha ficado claro, informe!
. Caso não tenha ficado claro, informe!







