 por Pessoa Estranha » Ter Nov 25, 2014 12:57
por Pessoa Estranha » Ter Nov 25, 2014 12:57
Olá, pessoal! Boa tarde!
Preciso de ajuda para o seguinte exercício:
"Prove que

é subgrupo normal de
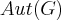
."
Antes disso, o exercício pede para provar que é um automorfismo de G a

definida por
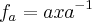
, para cada

,

. Essa parte eu consegui mostrar. Também provei que I(G) é subgrupo, mas não estou conseguindo mostrar que é normal.
Por favor, podem ajudar?
Muito Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por adauto martins » Seg Dez 01, 2014 16:40
por adauto martins » Seg Dez 01, 2014 16:40
seja
![y\in G /y.{f}_{a}=[y.(a.x.{a}^{-1})]=[(a.x.{a}^{-1}).y]={f}_{a}.y... y\in G /y.{f}_{a}=[y.(a.x.{a}^{-1})]=[(a.x.{a}^{-1}).y]={f}_{a}.y...](/latexrender/pictures/7cdc3063c7272862968d2ab93e25bd09.png)
as classes laterais a direita sao as mesma das classes laterais a esquerda,logo I(G) e normal a G
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Estruturas Algébricas] Operações - Exercício
por Pessoa Estranha » Ter Set 16, 2014 14:01
- 2 Respostas
- 2163 Exibições
- Última mensagem por Pessoa Estranha

Ter Set 30, 2014 15:36
Álgebra Elementar
-
- [Estruturas Algébricas] Operações - Outro Exercício
por Pessoa Estranha » Ter Set 16, 2014 14:06
- 2 Respostas
- 1545 Exibições
- Última mensagem por adauto martins

Dom Set 28, 2014 16:28
Álgebra Elementar
-
- Estruturas algébricas
por Eliane Maria » Qua Abr 25, 2012 01:01
- 12 Respostas
- 9165 Exibições
- Última mensagem por fraol

Ter Mai 01, 2012 23:42
Álgebra Elementar
-
- Anéis ( Estruturas algébricas)
por Crist » Qui Mar 20, 2014 15:32
- 1 Respostas
- 2889 Exibições
- Última mensagem por adauto martins

Seg Mar 14, 2016 19:47
Teoria dos Números
-
- [Estruturas algébricas] Anéis
por Crist » Sáb Mar 22, 2014 16:45
- 1 Respostas
- 2087 Exibições
- Última mensagem por adauto martins

Ter Jan 13, 2015 15:45
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 é subgrupo normal de
é subgrupo normal de 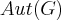 ."
." definida por
definida por 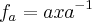 , para cada
, para cada  ,
,  . Essa parte eu consegui mostrar. Também provei que I(G) é subgrupo, mas não estou conseguindo mostrar que é normal.
. Essa parte eu consegui mostrar. Também provei que I(G) é subgrupo, mas não estou conseguindo mostrar que é normal. 

![y\in G /y.{f}_{a}=[y.(a.x.{a}^{-1})]=[(a.x.{a}^{-1}).y]={f}_{a}.y... y\in G /y.{f}_{a}=[y.(a.x.{a}^{-1})]=[(a.x.{a}^{-1}).y]={f}_{a}.y...](/latexrender/pictures/7cdc3063c7272862968d2ab93e25bd09.png)
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)