Potenciação

por **Mateus Mataveli** » Qui Nov 06, 2014 00:39

Oi gente, por favor me ajudem neste exercício, ele é simples, porém nao consigo entender como se desenvolve, olhei algumas explicações mas acabei me confundindo ainda mais. O exercício é o seguinte:

O algarismo das unidades de 2013^2014 (2013 elevado a 2014) é:

a) 1
B) 3
C) 4
d) 7
E) 9

Existe alguma formula? Desde ja agradeço!

por **adauto martins** » Sex Nov 07, 2014 10:21

para resolver esse exercicio teremos q. primeiro provar:
9 elevado a uma potencia par,tera na casa das unidades o numero 1...9 elevado a uma potencia impar,tera na casa das unidades o numero 9...fica como exercicio a prova...vamos a soluçao:
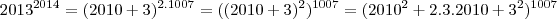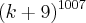${2013}^{2014}=({2010+3})^{2.1007}=({({2010+3})^{2}})^{1007}=({{2010}^{2}+2.3.2010+{3}^{2}})^ {1007}$ = $({k+9})^{1007}$ ,expandindo a expressao em um binomio de newto,teremos:
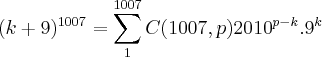$({k+9})^{1007}=\sum_{1}^{1007}C(1007,p){2010}^{p-k}.{9}^{k}$ ,onde C(1007,K)=1007!/(k!(1007-k)!)...logo teremos: 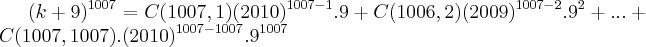$({k+9})^{1007}=C(1007,1)({2010})^{1007-1}.9+C(1006,2)({2009})^{1007-2}.{9}^{2}+...+C(1007,1007).({2010})^{1007-1007}.{9}^{1007}$ ,como 1007 e um numero impar,entao a casa das unidades tera o numero 9...