 por IlgssonBraga » Sáb Jul 26, 2014 15:30
por IlgssonBraga » Sáb Jul 26, 2014 15:30
Sejam
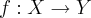
e
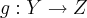
funções. Demonstre que:
Se gof é injetora e f é sobrejetora, então g é injetora. Onde gof=g(f(x)).
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
 por ant_dii » Sáb Jul 26, 2014 16:32
por ant_dii » Sáb Jul 26, 2014 16:32
Por definição, como

é sobrejetora, para qualquer
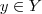
existe, pelo menos, um

tal que

.
Também por definição, como

é injetora segue que para
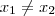
em

implica que
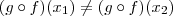
em

.
Mas

e

para
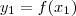
e
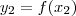
.
Logo,
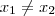
em

implica que

em

, ou seja,

é injetora. Note que

"cobre" todos os elementos de

, por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de

.
Só os loucos sabem...
-
ant_dii
- Colaborador Voluntário

-
- Mensagens: 129
- Registrado em: Qua Jun 29, 2011 19:46
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matemática
- Andamento: formado
 por IlgssonBraga » Sáb Jul 26, 2014 16:42
por IlgssonBraga » Sáb Jul 26, 2014 16:42
Muito obrigado !!!
-
IlgssonBraga
- Usuário Ativo

-
- Mensagens: 18
- Registrado em: Qui Jul 18, 2013 10:07
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Função - Como proceder nesse caso?
por micheel » Dom Ago 18, 2013 22:37
- 1 Respostas
- 1993 Exibições
- Última mensagem por Russman

Dom Ago 18, 2013 23:16
Funções
-
- Como proceder... estou com duvidas...
por Netolucena » Dom Mar 18, 2012 18:32
- 2 Respostas
- 1667 Exibições
- Última mensagem por Netolucena

Dom Mar 18, 2012 22:06
Cálculo: Limites, Derivadas e Integrais
-
- analise real como proceder
por caciano-death » Sex Ago 25, 2017 17:56
- 2 Respostas
- 2129 Exibições
- Última mensagem por adauto martins

Qua Ago 30, 2017 11:36
Cálculo: Limites, Derivadas e Integrais
-
- Como resolvo problemas desse tipo?
por PriscilaMG » Dom Nov 22, 2009 12:25
- 1 Respostas
- 1900 Exibições
- Última mensagem por PriscilaMG

Dom Nov 22, 2009 12:33
Logaritmos
-
- como resolver esse tipo de conta?
por LuizCarlos » Seg Jul 11, 2011 00:43
- 11 Respostas
- 6176 Exibições
- Última mensagem por LuizCarlos

Ter Jul 12, 2011 20:00
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
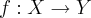 e
e 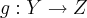 funções. Demonstre que:
funções. Demonstre que:
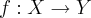 e
e 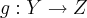 funções. Demonstre que:
funções. Demonstre que:
 é sobrejetora, para qualquer
é sobrejetora, para qualquer 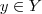 existe, pelo menos, um
existe, pelo menos, um  tal que
tal que  .
. é injetora segue que para
é injetora segue que para 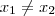 em
em  implica que
implica que 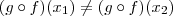 em
em  .
. e
e  para
para 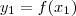 e
e 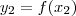 .
.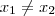 em
em  implica que
implica que  em
em  , ou seja,
, ou seja,  é injetora. Note que
é injetora. Note que  "cobre" todos os elementos de
"cobre" todos os elementos de  , por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de
, por ser sobrejetora ,portanto a implicação acima vale para qualquer elemento de  .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.