 por IsadoraLG » Qua Jul 09, 2014 21:47
por IsadoraLG » Qua Jul 09, 2014 21:47
Nesse caso, só fiquei em dúvida quanto a um passo do exercício:
(UNIFOR) Os números reais a e b, que satifazem a igualdade
![({\sqrt[]{3} + 1})^{4} = a + b\sqrt[]{3} ({\sqrt[]{3} + 1})^{4} = a + b\sqrt[]{3}](/latexrender/pictures/0389e2e3d25565a32e816fd73fde03de.png)
, são tais que a - b é igual a:
A)12
B)14
C)15
D)18
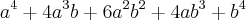
![{\sqrt[]{3}}^{4} + {\sqrt[]{3}}^{3} . 1+6 ({\sqrt[]{3}})^{2}+{1}^{2} + 4{\sqrt[]{3}}^{3} . 1 + {1}^{4} {\sqrt[]{3}}^{4} + {\sqrt[]{3}}^{3} . 1+6 ({\sqrt[]{3}})^{2}+{1}^{2} + 4{\sqrt[]{3}}^{3} . 1 + {1}^{4}](/latexrender/pictures/1198c916c6daaede60db964c8b59b926.png)
Com estas contas, chegamos a >>>
![({\sqrt[]{3}}^{} . \sqrt[]{3}) ({\sqrt[]{3}}^{} . \sqrt[]{3})](/latexrender/pictures/780004254ec53db8a41b976979942406.png)
:
![3 . 3 + 4 . 3\sqrt[]{3}+ 6 . 3 + 4\sqrt[]{3}+1 >>>> 3 . 3 + 4 . 3\sqrt[]{3}+ 6 . 3 + 4\sqrt[]{3}+1 >>>>](/latexrender/pictures/9aad387f7df7c14d72f04718b1cb34df.png)
>>>> É nessa linha que entra minha dúvida: onde está, o que aconteceu com o
![{\sqrt[]{3} }^{3} {\sqrt[]{3} }^{3}](/latexrender/pictures/b0250ab3afa8adb1cf2b0abeeab57fb9.png)
da linha anterior?....
-
IsadoraLG
- Usuário Ativo

-
- Mensagens: 21
- Registrado em: Ter Ago 27, 2013 18:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Gestão em Recursos Humanos
- Andamento: formado
 por DanielFerreira » Qua Jul 16, 2014 20:41
por DanielFerreira » Qua Jul 16, 2014 20:41
Isadora, não estou mui certo se entendi sua dúvida, mas...

Poderíamos também resolvê-la da seguinte forma:

Ora, temos então

e

.
Logo,
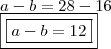
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Talvez fatoração, mas não consegui desenvolver
por IsadoraLG » Qua Jul 09, 2014 21:13
- 1 Respostas
- 1192 Exibições
- Última mensagem por e8group

Qui Jul 10, 2014 00:58
Álgebra Elementar
-
- [Função F] Não consigo desenvolver esse exercício
por thayna_rosa » Seg Nov 12, 2012 18:35
- 4 Respostas
- 2328 Exibições
- Última mensagem por thayna_rosa

Seg Nov 12, 2012 20:58
Funções
-
- [Equação Irracional] - Como desenvolver esse exercício?
por Crouff » Qui Jul 05, 2012 11:55
- 2 Respostas
- 1846 Exibições
- Última mensagem por Crouff

Qui Jul 05, 2012 12:29
Sistemas de Equações
-
- Fatoração - consegui fazer apenas o óbvio
por IsadoraLG » Qua Jul 09, 2014 21:19
- 1 Respostas
- 1396 Exibições
- Última mensagem por e8group

Qui Jul 10, 2014 02:12
Álgebra Elementar
-
- [Fatoração] Não estou conseguindo resolver esse exercício
por Ze Birosca » Qua Fev 04, 2015 18:55
- 4 Respostas
- 3008 Exibições
- Última mensagem por Ze Birosca

Qua Fev 04, 2015 21:56
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 5 visitantes
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Thassya - Sáb Out 01, 2011 16:20
1) Para que os pontos (1,3) e (-3,1) pertençam ao grafico da função f(X)=ax + b ,o valor de b-a deve ser ?
2)Qual o maior valor assumido pela função f : [-7 ,10] em R definida por f(x) = x ao quadrado - 5x + 9?
3) A função f, do primeiro grau, é definida pos f(x)= 3x + k para que o gráfico de f corte o eixo das ordenadas no ponto de ordenada 5 é?
Assunto:
[Função] do primeiro grau e quadratica
Autor:
Neperiano - Sáb Out 01, 2011 19:46
Ola
Qual as suas dúvidas?
O que você não está conseguindo fazer?
Nos mostre para podermos ajudar
Atenciosamente
Assunto:
[Função] do primeiro grau e quadratica
Autor:
joaofonseca - Sáb Out 01, 2011 20:15
1)Dados dois pontos A=(1,3) e B=(-3,1) de uma reta, é possivel definir a sua equação.


Em

substitui-se
m, substitui-se
y e
x por um dos pares ordenados, e resolve-se em ordem a
b.

2)Na equação

não existem zeros.Senão vejamos
Completando o quadrado,

As coordenadas do vertice da parabola são

O eixo de simetria é a reta

.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
f(-7)=93
f(10)=59
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![({\sqrt[]{3} + 1})^{4} = a + b\sqrt[]{3} ({\sqrt[]{3} + 1})^{4} = a + b\sqrt[]{3}](/latexrender/pictures/0389e2e3d25565a32e816fd73fde03de.png) , são tais que a - b é igual a:
, são tais que a - b é igual a: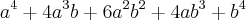
![{\sqrt[]{3}}^{4} + {\sqrt[]{3}}^{3} . 1+6 ({\sqrt[]{3}})^{2}+{1}^{2} + 4{\sqrt[]{3}}^{3} . 1 + {1}^{4} {\sqrt[]{3}}^{4} + {\sqrt[]{3}}^{3} . 1+6 ({\sqrt[]{3}})^{2}+{1}^{2} + 4{\sqrt[]{3}}^{3} . 1 + {1}^{4}](/latexrender/pictures/1198c916c6daaede60db964c8b59b926.png)
![({\sqrt[]{3}}^{} . \sqrt[]{3}) ({\sqrt[]{3}}^{} . \sqrt[]{3})](/latexrender/pictures/780004254ec53db8a41b976979942406.png) :
:![3 . 3 + 4 . 3\sqrt[]{3}+ 6 . 3 + 4\sqrt[]{3}+1 >>>> 3 . 3 + 4 . 3\sqrt[]{3}+ 6 . 3 + 4\sqrt[]{3}+1 >>>>](/latexrender/pictures/9aad387f7df7c14d72f04718b1cb34df.png) >>>> É nessa linha que entra minha dúvida: onde está, o que aconteceu com o
>>>> É nessa linha que entra minha dúvida: onde está, o que aconteceu com o ![{\sqrt[]{3} }^{3} {\sqrt[]{3} }^{3}](/latexrender/pictures/b0250ab3afa8adb1cf2b0abeeab57fb9.png) da linha anterior?....
da linha anterior?....



 e
e  .
.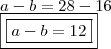



 substitui-se
substitui-se 
 não existem zeros.Senão vejamos
não existem zeros.Senão vejamos

 .Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.
.Como se pode observar o vertice está acima do eixo Ox, estando parabola virada para cima, o vertice é um mínimo absoluto.Então basta calcular a função para os valores dos extremos do intervalo.