 por Gladimir » Ter Fev 04, 2014 21:51
por Gladimir » Ter Fev 04, 2014 21:51
Como se faz essa professor:
Considere que, em uma empresa, há máquinas copiadoras do tipo A e do tipo B, nas seguintes condições:
• 3 máquinas do tipo A, funcionando conjuntamente com 2 máquinas do tipo B, produzem 13.920 cópias, ao todo,
em meia hora;
• todas as máquinas do tipo A funcionam sob um mesmo regime constante;
• todas as máquinas do tipo B funcionam sob um mesmo regime constante, 40% maior do que o regime das
máquinas do tipo A.
O número de cópias por minuto, nessa empresa, que uma máquina do tipo B faz a mais do que uma máquina do tipo
A é:
-
Gladimir
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 31, 2014 23:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Filosofia
- Andamento: formado
 por Gladimir » Qua Fev 05, 2014 10:41
por Gladimir » Qua Fev 05, 2014 10:41
Porque vc sumiu com B nessa parte da questão: Só essa parte ainda não entendi!
3.A+2.1,4.B=464
5,8.A=464
-
Gladimir
- Novo Usuário

-
- Mensagens: 8
- Registrado em: Sex Jan 31, 2014 23:30
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Filosofia
- Andamento: formado
 por young_jedi » Qui Fev 06, 2014 18:37
por young_jedi » Qui Fev 06, 2014 18:37
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Problema
por fabio muniz » Qui Out 23, 2008 16:14
- 1 Respostas
- 10715 Exibições
- Última mensagem por admin

Ter Out 28, 2008 17:47
Problemas do Cotidiano
-
- Problema
por Lima » Dom Dez 14, 2008 18:08
- 3 Respostas
- 9727 Exibições
- Última mensagem por blangis

Dom Dez 14, 2008 20:15
Sistemas de Equações
-
- Problema..
por ANDRE RENATO PROFETA » Sex Mar 13, 2009 00:36
- 1 Respostas
- 3314 Exibições
- Última mensagem por Molina

Sex Mar 13, 2009 14:58
Álgebra Elementar
-
- Problema
por ginrj » Qua Jun 03, 2009 19:19
- 3 Respostas
- 4608 Exibições
- Última mensagem por Cleyson007

Dom Jun 07, 2009 11:48
Álgebra Elementar
-
- Problema. . .
por Fernanda90 » Qui Ago 27, 2009 20:36
- 3 Respostas
- 6530 Exibições
- Última mensagem por Elcioschin

Qui Ago 27, 2009 22:27
Estatística
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



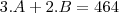
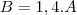
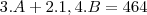


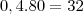

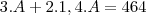

 .
.
 :
: