 por dummyman » Sáb Jan 04, 2014 12:28
por dummyman » Sáb Jan 04, 2014 12:28
Oi pessoal, esse eh meu primeiro post aqui no fórum.
Tenho a seguinte equação:
N+1=1+b+(b^2)+...+(b^d)
Sei que N vale 52 e d vale 5.
Gostaria de saber como proceder para encontrar o valor de b.
Fico muito grato a quem puder ajudar.
-
dummyman
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sáb Jan 04, 2014 12:11
- Formação Escolar: GRADUAÇÃO
- Área/Curso: TI
- Andamento: formado
 por e8group » Sáb Jan 04, 2014 15:26
por e8group » Sáb Jan 04, 2014 15:26
Note que a soma ao lado direito da igualdade é a soma dos

primeiros termos da sequência (neste caso P.G de razão b)

. A sequência

és uma P.G. de razão

e a soma dos primeiros

termos é dada por

e assim

. Ou seja,

e portanto

desde que
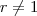
. Pela fórmula destacada ,temos

. O número

corresponde a uma solução real da eq.

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Russman » Seg Jan 06, 2014 01:24
por Russman » Seg Jan 06, 2014 01:24
Também a própria fórmula já é uma equação donde se é capaz de calcular o(s) valor(es) de

.
Veja que

reduz -se a

que é uma equação polinomial de grau 5.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [ALGEBRA LINEAR] Equação com Matriz e Somatório
por kpug » Ter Out 23, 2012 20:55
- 0 Respostas
- 1928 Exibições
- Última mensagem por kpug

Ter Out 23, 2012 20:55
Álgebra Linear
-
- (Potencia) equação com potencia
por Thiago1986Iz » Dom Jul 24, 2016 12:53
- 1 Respostas
- 2038 Exibições
- Última mensagem por DanielFerreira

Dom Jul 24, 2016 16:00
Equações
-
- [potência] equação
por Ederson_ederson » Qui Jun 25, 2015 08:49
- 1 Respostas
- 1946 Exibições
- Última mensagem por DanielFerreira

Sáb Jun 27, 2015 14:42
Álgebra Elementar
-
- [Equação] Potência no denominador
por manoelcarlos » Sex Ago 23, 2013 01:21
- 5 Respostas
- 2874 Exibições
- Última mensagem por manoelcarlos

Seg Ago 26, 2013 15:07
Equações
-
- [Série de potÊncia] Expansão de séries de potência
 por Adonias 7 » Qua Jun 01, 2016 09:05
por Adonias 7 » Qua Jun 01, 2016 09:05
- 0 Respostas
- 3686 Exibições
- Última mensagem por Adonias 7

Qua Jun 01, 2016 09:05
Sequências
Usuários navegando neste fórum: Nenhum usuário registrado e 6 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 primeiros termos da sequência (neste caso P.G de razão b)
primeiros termos da sequência (neste caso P.G de razão b)  . A sequência
. A sequência  és uma P.G. de razão
és uma P.G. de razão  e a soma dos primeiros
e a soma dos primeiros  termos é dada por
termos é dada por  e assim
e assim  . Ou seja,
. Ou seja,  e portanto
e portanto  desde que
desde que 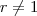 . Pela fórmula destacada ,temos
. Pela fórmula destacada ,temos  . O número
. O número  corresponde a uma solução real da eq.
corresponde a uma solução real da eq. 

 .
.



 .
.



