 por Valmel » Dom Jul 28, 2013 11:46
por Valmel » Dom Jul 28, 2013 11:46
Considere o número n = 672 .
É CORRETO afrmar que o número n termina com
a) 16.
b) 96.
c) 56.
d) 36.
gabarito: 36
Vi um comentário que explica (não coloquei o sinal mas é potenciação,desculpa)
61=6 66=46656
62=36 67=279936
63=216 68=1679616
64=1296 69=10077696
65=7776 610=60466176
Do comentário do colega ainda não consegui entender de qual premissa vou partir pra deduzir em que N o número termina?
-
Valmel
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Qui Set 27, 2012 17:59
- Localização: Ceará
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por MateusL » Dom Jul 28, 2013 17:45
por MateusL » Dom Jul 28, 2013 17:45
Valmel , não consegui entender o exercício.
Por favor, escreva as expressões utilizando o
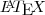 Clique aqui
Clique aqui para ler o tópico com as instruções para utilizar o
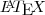
.
-
MateusL
- Usuário Parceiro

-
- Mensagens: 68
- Registrado em: Qua Jul 17, 2013 23:25
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- CESPE-ANCINE-2006-Analista administrativo
por Valmel » Dom Jul 28, 2013 11:25
- 2 Respostas
- 1642 Exibições
- Última mensagem por Valmel

Dom Jul 28, 2013 22:49
Álgebra Elementar
-
- Pm-Es(2011)
por DanielRJ » Sex Dez 23, 2011 19:19
- 5 Respostas
- 3488 Exibições
- Última mensagem por fraol

Seg Dez 26, 2011 19:29
Geometria Espacial
-
- UNEB 2011
por zenildo » Seg Nov 11, 2013 09:36
- 0 Respostas
- 786 Exibições
- Última mensagem por zenildo

Seg Nov 11, 2013 09:36
Análise Combinatória
-
- UNEB 2011
por zenildo » Seg Nov 11, 2013 09:46
- 0 Respostas
- 1113 Exibições
- Última mensagem por zenildo

Seg Nov 11, 2013 09:46
Probabilidade
-
- Simulado ENEM 2011 - JÁ RESPONDIDO Vlw
 por Kelvin Brayan » Dom Abr 17, 2011 00:09
por Kelvin Brayan » Dom Abr 17, 2011 00:09
- 9 Respostas
- 7350 Exibições
- Última mensagem por Molina

Dom Abr 17, 2011 17:37
Progressões
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


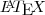



 , avisa que eu resolvo.
, avisa que eu resolvo.

