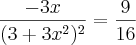 .
.

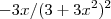 como
como ![-x/[3(x^2+1)^2] -x/[3(x^2+1)^2]](/latexrender/pictures/4c6f0a02d5740fcaf4becb907a397f8a.png) e considerando este resultado uma função
e considerando este resultado uma função  .Observando que o denominador é sempre positivo para quaisquer
.Observando que o denominador é sempre positivo para quaisquer  real ,então comparando a igualdade dada (equação) é fácil ver que se
real ,então comparando a igualdade dada (equação) é fácil ver que se  admite um número finito de soluções reais ,então obrigatoriamente tais soluções são
admite um número finito de soluções reais ,então obrigatoriamente tais soluções são  ,mas isto contradiz o teorema do valor intermediário (TVI) , pois
,mas isto contradiz o teorema do valor intermediário (TVI) , pois  é contínua em
é contínua em  e
e 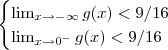 o que implica que não existe
o que implica que não existe  em quaisquer intervalos
em quaisquer intervalos ![[M,N] \subset (-\infty,0) [M,N] \subset (-\infty,0)](/latexrender/pictures/af2eb4470c1b5710264ebcc15f00d687.png) (ou
(ou ![[N,M] \subset (-\infty,0) ) [N,M] \subset (-\infty,0) )](/latexrender/pictures/f4f0100c56e6c0a8d17ddab86d7e0c76.png) tais que
tais que  .Logo pelo (TVI), concluímos que a suposição de
.Logo pelo (TVI), concluímos que a suposição de  admite um número finito de soluções reais é falsa ,i.e,a equação não admite solução real .
admite um número finito de soluções reais é falsa ,i.e,a equação não admite solução real .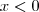 ,fazendo a substituição trigonométrica
,fazendo a substituição trigonométrica 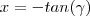 para
para 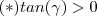 ,temos :
,temos : 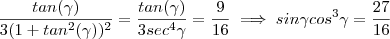 .Esta igualdade é uma contradição .Pois
.Esta igualdade é uma contradição .Pois 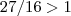 e as funções seno e cosseno são limitadas , pela hipótese
e as funções seno e cosseno são limitadas , pela hipótese tem-se
tem-se 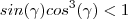 .Absurdo ! .
.Absurdo ! .
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
