 por anneliesero » Sáb Abr 27, 2013 22:46
por anneliesero » Sáb Abr 27, 2013 22:46
Olá, pessoal
poderia me ajudar aqui? Travei neste exercício e não estou conseguindo achar o resultado.
![\sqrt[]{\frac{a\sqrt[]{b}}{\sqrt[3]{ab}}}.\sqrt[4]{b} \sqrt[]{\frac{a\sqrt[]{b}}{\sqrt[3]{ab}}}.\sqrt[4]{b}](/latexrender/pictures/1be02f2b2d16f04ba9099bc98be53451.png)
O resultado é
![\sqrt[3]{ab} \sqrt[3]{ab}](/latexrender/pictures/b75c3a13b63e2969ab696ba4b2579ab6.png)
.
Fiz assim:
![\frac{\sqrt[2]{a\sqrt[2]{b}}}{\sqrt[2]{\sqrt[3]{ab}}}
\frac{\sqrt[2]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}
\frac{\sqrt[4]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}} \frac{\sqrt[2]{a\sqrt[2]{b}}}{\sqrt[2]{\sqrt[3]{ab}}}
\frac{\sqrt[2]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}
\frac{\sqrt[4]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}](/latexrender/pictures/115e604b9f72482bdf126d3cc9bc6fa2.png)
Não sei porque deu esse erro mas é dividido.
''Não confunda jamais conhecimento com sabedoria. Um o ajuda a ganhar a vida; o outro a construir uma vida.'' - Sandra Carey
-
anneliesero
- Usuário Parceiro

-
- Mensagens: 86
- Registrado em: Qui Set 13, 2012 17:58
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por e8group » Sáb Abr 27, 2013 23:48
por e8group » Sáb Abr 27, 2013 23:48
Note que
![\sqrt[4]{b} = \sqrt{\sqrt{b}} \sqrt[4]{b} = \sqrt{\sqrt{b}}](/latexrender/pictures/e71547184630650fb0b3059dfaa296e9.png)
.
Assim ,
![\sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}}\sqrt{\sqrt{b}} = \sqrt{\frac{a\sqrt{b} \cdot \sqrt{b} }{\sqrt[3]{ab}}} = \sqrt{\frac{ab}{\sqrt[3]{ab}}} \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}}\sqrt{\sqrt{b}} = \sqrt{\frac{a\sqrt{b} \cdot \sqrt{b} }{\sqrt[3]{ab}}} = \sqrt{\frac{ab}{\sqrt[3]{ab}}}](/latexrender/pictures/7b215c536b033d611cd9fc993a55ed3f.png)
.
Multiplicando-se em cima e em baixo dentro do radical por
![\sqrt[3]{(ab)^2} \sqrt[3]{(ab)^2}](/latexrender/pictures/4be179f3c753c1144909a839b83bbdcb.png)
segue o resultado .
Outra forma seria reescrever o radical em potência com o expoente fracionário .
Temos :
i)
![\sqrt[4]{b} = b^{1/4} \sqrt[4]{b} = b^{1/4}](/latexrender/pictures/2d9597e81d3c558148586b292ad712ac.png)
ii)
![\sqrt[3]{ab} = (ab)^{1/3} = a^{1/3} \cdot b^{1/3} \sqrt[3]{ab} = (ab)^{1/3} = a^{1/3} \cdot b^{1/3}](/latexrender/pictures/5143c0fceaf5b9045e37859568efe20a.png)
iii)

.
iv)
![\sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} = \sqrt{\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}} = \left(\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}\right)^{1/2} = \left(\frac{b^{1/2} }{b^{1/3}} \cdot \frac{a}{a^{1/3}}\right)^{1/2} = \left(b^{1/2 - 1/3} \cdot a^{1-1/3}\right)^{1/2} = (b^{1/6} a^{2/3})^{1/2} =(b^{1/6})^{1/2} \cdot (a^{2/3})^{1/2} = b^{1/12} a^{1/3} \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} = \sqrt{\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}} = \left(\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}\right)^{1/2} = \left(\frac{b^{1/2} }{b^{1/3}} \cdot \frac{a}{a^{1/3}}\right)^{1/2} = \left(b^{1/2 - 1/3} \cdot a^{1-1/3}\right)^{1/2} = (b^{1/6} a^{2/3})^{1/2} =(b^{1/6})^{1/2} \cdot (a^{2/3})^{1/2} = b^{1/12} a^{1/3}](/latexrender/pictures/7917e8ed2b62b98a44f9889e034e463d.png)
Daí ,
![\sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = b^{1/12} a^{1/3} b^{1/4} = b^{1/12 +1/4} a^{1/3} = b^{4/12} a^{1/3} = b^{1/3} a^{1/3} = (ab)^{1/3} = \sqrt[3]{ab} \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = b^{1/12} a^{1/3} b^{1/4} = b^{1/12 +1/4} a^{1/3} = b^{4/12} a^{1/3} = b^{1/3} a^{1/3} = (ab)^{1/3} = \sqrt[3]{ab}](/latexrender/pictures/23a47004324e88c0b8de60364cbc12f0.png)
Infelizmente não conseguir visualizar a sua resolução por causa da configuração com o
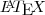
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Potenciação e Radiciação
por Carlos22 » Qua Abr 13, 2011 22:06
- 1 Respostas
- 1922 Exibições
- Última mensagem por FilipeCaceres

Qua Abr 13, 2011 22:27
Logaritmos
-
- [Potenciação e radiciação]
por SCHOOLGIRL+T » Qua Nov 07, 2012 21:19
- 4 Respostas
- 2658 Exibições
- Última mensagem por SCHOOLGIRL+T

Sex Nov 09, 2012 23:44
Álgebra Elementar
-
- [Potenciação e Radiciação]
por JU201015 » Seg Nov 12, 2012 22:06
- 2 Respostas
- 1945 Exibições
- Última mensagem por JU201015

Ter Nov 13, 2012 09:08
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:51
- 1 Respostas
- 1244 Exibições
- Última mensagem por young_jedi

Dom Abr 28, 2013 21:20
Álgebra Elementar
-
- Potenciação e radiciação
por anneliesero » Sáb Abr 27, 2013 22:53
- 1 Respostas
- 1123 Exibições
- Última mensagem por nakagumahissao

Dom Abr 28, 2013 02:42
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{\frac{a\sqrt[]{b}}{\sqrt[3]{ab}}}.\sqrt[4]{b} \sqrt[]{\frac{a\sqrt[]{b}}{\sqrt[3]{ab}}}.\sqrt[4]{b}](/latexrender/pictures/1be02f2b2d16f04ba9099bc98be53451.png)
![\sqrt[3]{ab} \sqrt[3]{ab}](/latexrender/pictures/b75c3a13b63e2969ab696ba4b2579ab6.png) .
. ![\frac{\sqrt[2]{a\sqrt[2]{b}}}{\sqrt[2]{\sqrt[3]{ab}}}
\frac{\sqrt[2]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}
\frac{\sqrt[4]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}} \frac{\sqrt[2]{a\sqrt[2]{b}}}{\sqrt[2]{\sqrt[3]{ab}}}
\frac{\sqrt[2]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}
\frac{\sqrt[4]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}](/latexrender/pictures/115e604b9f72482bdf126d3cc9bc6fa2.png)

![\sqrt[]{\frac{a\sqrt[]{b}}{\sqrt[3]{ab}}}.\sqrt[4]{b} \sqrt[]{\frac{a\sqrt[]{b}}{\sqrt[3]{ab}}}.\sqrt[4]{b}](/latexrender/pictures/1be02f2b2d16f04ba9099bc98be53451.png)
![\sqrt[3]{ab} \sqrt[3]{ab}](/latexrender/pictures/b75c3a13b63e2969ab696ba4b2579ab6.png) .
. ![\frac{\sqrt[2]{a\sqrt[2]{b}}}{\sqrt[2]{\sqrt[3]{ab}}}
\frac{\sqrt[2]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}
\frac{\sqrt[4]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}} \frac{\sqrt[2]{a\sqrt[2]{b}}}{\sqrt[2]{\sqrt[3]{ab}}}
\frac{\sqrt[2]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}
\frac{\sqrt[4]{\sqrt[2]{b{a}^{2}}}}{\sqrt[6]{\sqrt[2]{ab}}}](/latexrender/pictures/115e604b9f72482bdf126d3cc9bc6fa2.png)

![\sqrt[4]{b} = \sqrt{\sqrt{b}} \sqrt[4]{b} = \sqrt{\sqrt{b}}](/latexrender/pictures/e71547184630650fb0b3059dfaa296e9.png) .
.![\sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}}\sqrt{\sqrt{b}} = \sqrt{\frac{a\sqrt{b} \cdot \sqrt{b} }{\sqrt[3]{ab}}} = \sqrt{\frac{ab}{\sqrt[3]{ab}}} \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}}\sqrt{\sqrt{b}} = \sqrt{\frac{a\sqrt{b} \cdot \sqrt{b} }{\sqrt[3]{ab}}} = \sqrt{\frac{ab}{\sqrt[3]{ab}}}](/latexrender/pictures/7b215c536b033d611cd9fc993a55ed3f.png) .
. ![\sqrt[3]{(ab)^2} \sqrt[3]{(ab)^2}](/latexrender/pictures/4be179f3c753c1144909a839b83bbdcb.png) segue o resultado .
segue o resultado .![\sqrt[4]{b} = b^{1/4} \sqrt[4]{b} = b^{1/4}](/latexrender/pictures/2d9597e81d3c558148586b292ad712ac.png)
![\sqrt[3]{ab} = (ab)^{1/3} = a^{1/3} \cdot b^{1/3} \sqrt[3]{ab} = (ab)^{1/3} = a^{1/3} \cdot b^{1/3}](/latexrender/pictures/5143c0fceaf5b9045e37859568efe20a.png)
 .
. ![\sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} = \sqrt{\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}} = \left(\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}\right)^{1/2} = \left(\frac{b^{1/2} }{b^{1/3}} \cdot \frac{a}{a^{1/3}}\right)^{1/2} = \left(b^{1/2 - 1/3} \cdot a^{1-1/3}\right)^{1/2} = (b^{1/6} a^{2/3})^{1/2} =(b^{1/6})^{1/2} \cdot (a^{2/3})^{1/2} = b^{1/12} a^{1/3} \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} = \sqrt{\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}} = \left(\frac{a b^{1/2} }{ a^{1/3} \cdot b^{1/3}}\right)^{1/2} = \left(\frac{b^{1/2} }{b^{1/3}} \cdot \frac{a}{a^{1/3}}\right)^{1/2} = \left(b^{1/2 - 1/3} \cdot a^{1-1/3}\right)^{1/2} = (b^{1/6} a^{2/3})^{1/2} =(b^{1/6})^{1/2} \cdot (a^{2/3})^{1/2} = b^{1/12} a^{1/3}](/latexrender/pictures/7917e8ed2b62b98a44f9889e034e463d.png)
![\sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = b^{1/12} a^{1/3} b^{1/4} = b^{1/12 +1/4} a^{1/3} = b^{4/12} a^{1/3} = b^{1/3} a^{1/3} = (ab)^{1/3} = \sqrt[3]{ab} \sqrt{\frac{a\sqrt{b}}{\sqrt[3]{ab}}} \sqrt[4]{b} = b^{1/12} a^{1/3} b^{1/4} = b^{1/12 +1/4} a^{1/3} = b^{4/12} a^{1/3} = b^{1/3} a^{1/3} = (ab)^{1/3} = \sqrt[3]{ab}](/latexrender/pictures/23a47004324e88c0b8de60364cbc12f0.png)
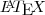

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.