Olá.
Não há uma única forma de resolver.
Antes, veja estes problemas semelhantes de idades:
viewtopic.php?f=97&t=128&p=218#p218viewtopic.php?f=19&t=38Se você entender corretamente, pode montar direto o sistema de equações.
Suas equações não estão corretas, então sugiro nestes problemas considerar uma "linha do tempo".
Não se preocupe com o sistema inicialmente, as equações surgirão naturalmente.
Escolha uma variável para a idade da pessoa mais nova, por exemplo,

.
Escreva para as duas pessoas, em forma de tabela, as idades "hoje" e no "futuro" (daqui a 2 anos).
Repare que para simplificar, você pode expressar todas as idades somente em relação a

, nem precisa colocar outra variável.
A idéia da tabela é esta, tente preencher:

Depois, com esta simples tabela preenchida, como o enunciado diz:
Daqui a dois anos, a mais velha tera o dobro da mais nova.
Iguale as idades do futuro e encontre

que é a idade da mais nova.
Então, olhe na tabela e obtenha a idade da mais velha no presente, uma vez que você já saberá o valor de

.
Para você conferir, as idades são 13 e 28 anos.
Espero ter ajudado!


 .
.



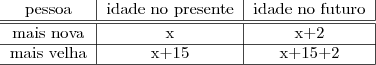


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.