 por replay » Qua Nov 21, 2012 11:24
por replay » Qua Nov 21, 2012 11:24
2- Fatore:

Estou tendo pesadas duvidas sobre os passos para se fatorar.
Primeiro sei que preciso pegar termos em comum.
Vejo que o +1 é o termo comum, pelo menos eu acho.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por DanielFerreira » Qua Nov 21, 2012 19:07
por DanielFerreira » Qua Nov 21, 2012 19:07
Replay,boa noite!
Trata-se de um
trinômio quadrado perfeito!
Exemplo I:
Ida.
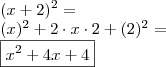
Exemplo II:
Volta.

replay escreveu:2- Fatore:

Estou tendo pesadas duvidas sobre os passos para se fatorar.
Primeiro sei que preciso pegar termos em comum.
Vejo que o +1 é o termo comum, pelo menos eu acho.
![\\ (a + 1)^2 + 2(a + 1) + 1 = \\\\ \left [ (a + 1) + 1]^2 = \right ] \\\\ (a + 1 + 1)^2 = \\\\ \boxed{\boxed{(a + 2)^2}} \\ (a + 1)^2 + 2(a + 1) + 1 = \\\\ \left [ (a + 1) + 1]^2 = \right ] \\\\ (a + 1 + 1)^2 = \\\\ \boxed{\boxed{(a + 2)^2}}](/latexrender/pictures/f250dc3d5e871bdc399b525a94ae905f.png)
Comente qualquer dúvida!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por ednaldo1982 » Qua Nov 21, 2012 21:19
por ednaldo1982 » Qua Nov 21, 2012 21:19
replay escreveu:2- Fatore:

Estou tendo pesadas duvidas sobre os passos para se fatorar.
Primeiro sei que preciso pegar termos em comum.
Vejo que o +1 é o termo comum, pelo menos eu acho.
CHAME (a + 1) de X:
Logo você terá:
X² + 2.
X + 1
Para se fatorar na forma do
trinômio quadrado perfeito, você verifica se o dobro do produto das raizes quadradas do primeiro e do terceiro termos é o mesmo valor do termo central.
Neste caso:
Raiz quadrada de X² = X
Raiz quadrada de 1 = 1
Dobro do produto das raizes:
2 .( x . 1) = 2x (que é igual ao termo central [
sem considerar o sinal] )
Portanto: Você teria (X + 1) . (X + 1) ou (X -1) . (X - 1) dependendo do sinal da função dada. Fazendo a distributiva você verifica qual das duas fica de acordo com o enunciado.
Logo, você teria:
(
X + 1)²
Porém, seu
X = (a +1)
Trocando
X por (a+1), temos:
(
a+1 + 1)² = (a + 2)²
Valeu!?
Um abraço, Professor Ednaldo Raposeiro
-

ednaldo1982
- Usuário Dedicado

-
- Mensagens: 44
- Registrado em: Seg Mar 26, 2012 11:28
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por replay » Qui Nov 22, 2012 09:31
por replay » Qui Nov 22, 2012 09:31
Entendi, o problema foi que acabei de estudar Fatoração com agrupamento e me cai que a primeira questão pede Trinomio Quadrado Perfeito, que é um conceito um pouco mais avançado.
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por replay » Seg Dez 10, 2012 17:21
por replay » Seg Dez 10, 2012 17:21
valeu acho que já consegui
-
replay
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Dom Fev 19, 2012 23:43
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Fatoração - consegui fazer apenas o óbvio
por IsadoraLG » Qua Jul 09, 2014 21:19
- 1 Respostas
- 1397 Exibições
- Última mensagem por e8group

Qui Jul 10, 2014 02:12
Álgebra Elementar
-
- como fazer?
por Amandatkm » Qui Mar 21, 2013 18:12
- 1 Respostas
- 2450 Exibições
- Última mensagem por timoteo

Qui Mar 21, 2013 20:56
Geometria Espacial
-
- não sei como fazer!!
por Lenin » Seg Jun 10, 2013 11:29
- 0 Respostas
- 1932 Exibições
- Última mensagem por Lenin

Seg Jun 10, 2013 11:29
Polinômios
-
- Tem como fazer sem a calculadora?
por Caroline Oliveyra » Ter Jul 12, 2011 22:18
- 1 Respostas
- 1974 Exibições
- Última mensagem por MarceloFantini

Qua Jul 13, 2011 04:11
Funções
-
- [Diagonalização] Como fazer?
por Alvadorn » Sáb Nov 10, 2012 17:12
- 1 Respostas
- 3003 Exibições
- Última mensagem por MarceloFantini

Sáb Nov 10, 2012 18:43
Álgebra
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




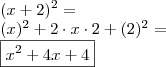

![\\ (a + 1)^2 + 2(a + 1) + 1 = \\\\ \left [ (a + 1) + 1]^2 = \right ] \\\\ (a + 1 + 1)^2 = \\\\ \boxed{\boxed{(a + 2)^2}} \\ (a + 1)^2 + 2(a + 1) + 1 = \\\\ \left [ (a + 1) + 1]^2 = \right ] \\\\ (a + 1 + 1)^2 = \\\\ \boxed{\boxed{(a + 2)^2}}](/latexrender/pictures/f250dc3d5e871bdc399b525a94ae905f.png)





 .
.



