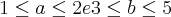 , pode-se afirmar que:
, pode-se afirmar que:Todas as alternativas estão em função de

Eu tinha feito
 e
e  , então...
, então... 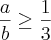 , mas isso é errado.
, mas isso é errado.A resposta correta é
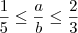

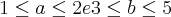 , pode-se afirmar que:
, pode-se afirmar que:
 e
e  , então...
, então... 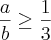 , mas isso é errado.
, mas isso é errado.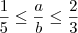






Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante


 , avisa que eu resolvo.
, avisa que eu resolvo.

