 por malbec » Qui Nov 22, 2012 10:12
por malbec » Qui Nov 22, 2012 10:12
Bom dia a todos os colegas desta página. Tenho uma dúvida para ser compartilhada aqui. Não consegui entender essa questão que me parece misturar função do 1º grau com radiciação. A questão é a seguinte: Dada a função f: C --> C onde f(x) = 3x + 7. Calcule
f(raiz de 7) - f(raiz de Pi)
raiz de 7 - raiz de Pi
as respostas foram as mais variadas, porém, a resposta certa foi a letra (A) 3.
Não consegui entender o sentido da questão e nem tampouco seus cálculos. Gostaria de ajuda se possível e agradeço desde já.
-
malbec
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 31, 2012 10:41
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: formação geral
- Andamento: cursando
 por e8group » Qui Nov 22, 2012 11:09
por e8group » Qui Nov 22, 2012 11:09
Dada a função
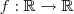
definida por
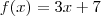
, calcule

. A função é esta mesma ?
Não faz sentido a resposta ser

, pois trata de uma operação de soma entre dois números irracionais , isto é ,

. Pela ordenação dos números reais , concluímos que ,
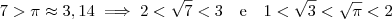
logo ,

Daí ,

e portanto

-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por e8group » Qui Nov 22, 2012 11:14
por e8group » Qui Nov 22, 2012 11:14
Não seria isto

???
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por malbec » Qui Nov 22, 2012 16:52
por malbec » Qui Nov 22, 2012 16:52
santhiago escreveu:Não seria isto

???
Boa tarde amigo Santiago! Seria essa mesmo a expressão, pois na verdade, eu não consegui colocar a expressão dessa forma aqui no quadro de dúvidas por causa das imagens. Gostaria de uma solução prática para esta questão. Agradeço desde já.
-
malbec
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 31, 2012 10:41
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: formação geral
- Andamento: cursando
 por e8group » Qui Nov 22, 2012 17:42
por e8group » Qui Nov 22, 2012 17:42
Vamos por partes ,
i)
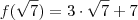
ii)

iii)
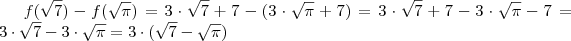
iv )
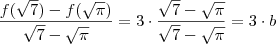
.
Para ficar compreensível vamos definir
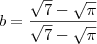
. Perceba que quanto o numerador e o denominador são composto por numeros iguais ,disso concluímos que b = 1 e portanto ,

.
Exemplos quanto que é
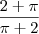
?
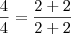
?

??
Códigos usados :
i)
- Código: Selecionar todos
f(\sqrt{7}) = 3 \cdot \sqrt{7} + 7
iii)
- Código: Selecionar todos
f(\sqrt{7}) - f(\sqrt{\pi}) = 3 \cdot \sqrt{7} + 7 - ( 3\cdot \sqrt{\pi} + 7 ) = 3 \cdot \sqrt{7} + 7 - 3\cdot \sqrt{\pi} - 7 = 3 \cdot \sqrt{7} - 3\cdot \sqrt{\pi} = 3 \cdot ( \sqrt{7} - \sqrt{\pi} )
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Radiciação
por thadeu » Qua Nov 18, 2009 16:32
- 1 Respostas
- 1696 Exibições
- Última mensagem por Elcioschin

Qua Nov 18, 2009 18:01
Álgebra Elementar
-
- Radiciaçao
por guillcn » Ter Abr 12, 2011 17:17
- 2 Respostas
- 2210 Exibições
- Última mensagem por guillcn

Ter Abr 12, 2011 18:05
Álgebra Elementar
-
- Radiciação
por marianne86 » Sex Set 02, 2011 02:05
- 1 Respostas
- 1158 Exibições
- Última mensagem por LuizAquino

Sex Set 02, 2011 11:16
Álgebra Elementar
-
- Radiciação
por TAE » Qua Mai 16, 2012 18:03
- 8 Respostas
- 4257 Exibições
- Última mensagem por DanielFerreira

Ter Mai 22, 2012 23:00
Álgebra Elementar
-
- Radiciacão
por anneliesero » Seg Jul 22, 2013 12:09
- 1 Respostas
- 1073 Exibições
- Última mensagem por temujin

Seg Jul 22, 2013 15:01
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


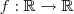 definida por
definida por 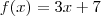 , calcule
, calcule  . A função é esta mesma ?
. A função é esta mesma ?  , pois trata de uma operação de soma entre dois números irracionais , isto é ,
, pois trata de uma operação de soma entre dois números irracionais , isto é ,  . Pela ordenação dos números reais , concluímos que ,
. Pela ordenação dos números reais , concluímos que , 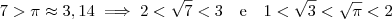 logo ,
logo , 
 e portanto
e portanto 

 ???
???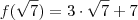

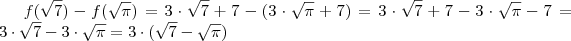
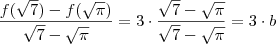 .
.  . Perceba que quanto o numerador e o denominador são composto por numeros iguais ,disso concluímos que b = 1 e portanto ,
. Perceba que quanto o numerador e o denominador são composto por numeros iguais ,disso concluímos que b = 1 e portanto ,  .
. 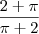 ?
? 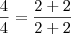 ?
? ??
?? .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
