 +2nx+n+2=0 tenham duas raizes reais distintas e maiores que zero devem pertencer ao intervalo:
+2nx+n+2=0 tenham duas raizes reais distintas e maiores que zero devem pertencer ao intervalo:A) (-
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) ,
,![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) ) B) (-infinito, -
) B) (-infinito, -![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) )União(
)União(![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) , +infinito) C) (-2, -
, +infinito) C) (-2, -![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) ) D) (
) D) (![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) , 2) E) (-2, 2)
, 2) E) (-2, 2) Bom pessol, quanto a resolução deste exercício, vou contar pra vocês o que eu já fiz.
Identifiquei que se trata de uma equação do segundo grau, portanto os coeficientes são a= (2-n) b=2n e c = (n+2)
Como queremos duas raizes reais e distintas, admitiremos que Delta deve ser maior que zero, resolvendo a expressão Delta, encontraremos dois valores de n, são eles:
n` =
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png)
n`` = -
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png)
Pois bem, ai é que começa meu problema, identificar qual o intervalo a que "n" deve pertencer para que as raízes desta equação, sejam além de distintas, positivas.
Ví uma resolução onde foi dito a seguinte afirmação:
"para que as raízes desta equação sejam maiores que zero, o produto e a soma entre elas, também devem ser."
Concordando com esta informação, tentei caminhar.
S = -b/2a
S = -2n/2-n>0
P = c/a
P = n+2/2-n>0
Mais não consigo sair daqui, não caminho.....
Observei que a resolução da pessoa que comentei acima, diz o seguinte, depois de resolver, "não sei como" as inequações acima:
Soma ele encontrou n<0
Produto ele encontrou n>-2
Com isto ele concluí que a resposta é que "n" deve pertencer ao intervalo (-2, -
![\sqrt[2]{2} \sqrt[2]{2}](/latexrender/pictures/a8f8ae3924f6c44624745ca9e588cae3.png) )!
)!É este o ponto amigos, não consigo entender o que este cara fez, me confundi e atrapalhei todo no momento que apareceram as inequações que fora,m geradas com as expressões de Soma e Produto.
Se puderem me orientar, agradeço


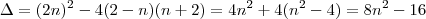 e isto deve ser maior que zero, logo
e isto deve ser maior que zero, logo 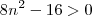 e
e  , portanto
, portanto 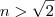 ou
ou  . Ou seja,
. Ou seja, 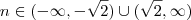 .
.


 .
.



