 por rnts » Seg Mai 21, 2012 16:15
por rnts » Seg Mai 21, 2012 16:15
Olá. Estava fazendo um exercício de Verdadeiro ou Falso, e fiquei em dúvida em um item.
'A soma de dois números irracionais pode ser racional.' Pensei que era falso, mas a resposta diz ser verdadeiro.
Fiquei um tempo tentando, mas não consigo demonstrar isso (nem pelo método direto nem indireto). Se alguém puder, agradeço.
-
rnts
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Sex Jan 27, 2012 12:06
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Guill » Sáb Mai 26, 2012 16:07
por Guill » Sáb Mai 26, 2012 16:07
Primeiramente, basta provar a seguinte proposição:
Seja x um número irranional que n um número racional. Dessa forma, (n + x) é irracional:
Suponhamos que (n + x) é racional. Dessa forma temos:

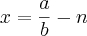
Logo x é racional, o que é um absurdo.
Agora, é lógico que:
![(1 - \sqrt[]{2}) + \sqrt[]{2} = 1 (1 - \sqrt[]{2}) + \sqrt[]{2} = 1](/latexrender/pictures/73ab39d5f4990b9541bf51cba9ec6f28.png)
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números irracionais
por cristina » Qua Set 16, 2009 23:40
- 1 Respostas
- 1972 Exibições
- Última mensagem por Marcampucio

Qui Set 17, 2009 00:18
Álgebra Elementar
-
- Números irracionais
por Marcia » Seg Nov 15, 2010 19:41
- 1 Respostas
- 1684 Exibições
- Última mensagem por Rogerio Murcila

Ter Nov 16, 2010 10:22
Álgebra Elementar
-
- números irracionais
por jose henrique » Sáb Fev 12, 2011 20:35
- 5 Respostas
- 5946 Exibições
- Última mensagem por Dan

Sáb Fev 12, 2011 21:39
Álgebra Elementar
-
- Números irracionais
por lacesar » Dom Abr 12, 2015 16:52
- 1 Respostas
- 2201 Exibições
- Última mensagem por adauto martins

Ter Mai 08, 2018 18:41
Cálculo: Limites, Derivadas e Integrais
-
- Números irracionais
por lacesar » Dom Abr 12, 2015 16:59
- 1 Respostas
- 1185 Exibições
- Última mensagem por adauto martins

Sáb Abr 18, 2015 12:06
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



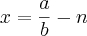
![(1 - \sqrt[]{2}) + \sqrt[]{2} = 1 (1 - \sqrt[]{2}) + \sqrt[]{2} = 1](/latexrender/pictures/73ab39d5f4990b9541bf51cba9ec6f28.png)

