Estou aqui vendo a resolução do livro nesse problema, mas não consegui entender como ele encontrou o valor
 .
.A hipotenusa de um triângulo retângulo tem
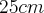 .Determine as medidas dos catetos desse triângulo sabendo que um deles mede
.Determine as medidas dos catetos desse triângulo sabendo que um deles mede  a mais que o outro.
a mais que o outro.Aplicando o teorema de Pitágoras:
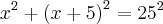
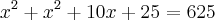
A única coisa que não estou conseguindo entender é de onde ele tirou esse
 . Como encontrou esse valor
. Como encontrou esse valor  .
.

 é um produto notável,
é um produto notável, 
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)