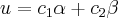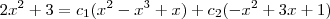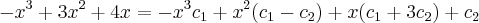por Ana_Rodrigues » Sáb Abr 28, 2012 16:21
por Ana_Rodrigues » Sáb Abr 28, 2012 16:21
Escreva se possível, os vetores

e

como combinação linear dos vetores

e

Alguém pode me ajudar com essa questão? não encontro um meio de resolvê-la.
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por MarceloFantini » Dom Abr 29, 2012 15:16
por MarceloFantini » Dom Abr 29, 2012 15:16
Você tentou escrever

,
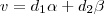
e a partir disso resolver para encontrar o valor das constantes?
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Ana_Rodrigues » Dom Abr 29, 2012 16:48
por Ana_Rodrigues » Dom Abr 29, 2012 16:48
eu comecei fazendo assim
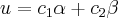
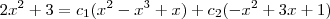

Daí eu não consegui achar alguma forma de provar que este vetor é ou não um subespaço gerado pelos vetores alfa e beta
Para o vetor v eu tenho:
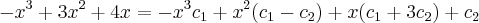
-
Ana_Rodrigues
- Usuário Parceiro

-
- Mensagens: 51
- Registrado em: Seg Nov 14, 2011 09:44
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- ESPAÇO LINEAR
por p1a2u3lo » Dom Set 18, 2016 11:01
- 0 Respostas
- 1383 Exibições
- Última mensagem por p1a2u3lo

Dom Set 18, 2016 11:01
Álgebra Linear
-
- espaço linear -dimensão
por futuro fisico » Sáb Jul 02, 2011 17:23
- 3 Respostas
- 4125 Exibições
- Última mensagem por Renato_RJ

Dom Jul 03, 2011 17:13
Álgebra
-
- Algebra Linear: Espaço Vetorial
por Caeros » Dom Nov 14, 2010 17:39
- 4 Respostas
- 5634 Exibições
- Última mensagem por andrefahl

Sáb Nov 27, 2010 18:16
Álgebra
-
- Algebra Linear - Espaço Vetorial
por Nillcolas » Qua Mar 16, 2011 17:05
- 1 Respostas
- 3953 Exibições
- Última mensagem por LuizAquino

Qua Mar 16, 2011 17:31
Álgebra
-
- [Ágebra Linear] Espaço Vetorial
por luisfelipefn » Seg Dez 08, 2014 22:54
- 1 Respostas
- 1836 Exibições
- Última mensagem por adauto martins

Qua Dez 10, 2014 11:49
Álgebra Linear
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  como combinação linear dos vetores
como combinação linear dos vetores  e
e 

 e
e  como combinação linear dos vetores
como combinação linear dos vetores  e
e 

 ,
, 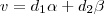 e a partir disso resolver para encontrar o valor das constantes?
e a partir disso resolver para encontrar o valor das constantes?