 por Cleyson007 » Sex Abr 13, 2012 15:27
por Cleyson007 » Sex Abr 13, 2012 15:27
Boa tarde a todos!

Estou tentando resolver assim:
Para n=1 a fórmula é válida, pois: n(n+1)(n+2)/3 = 2
Sei que devemos supor que a fórmula é válida para n, logo também será válida para (n+1).
Preciso de ajuda para prosseguir..
Aguardo retorno.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Guill » Sex Abr 13, 2012 16:11
por Guill » Sex Abr 13, 2012 16:11
Mas na verdade, não existia a necessidade de usar da indução:
1.2 + 2.3 + 3.4 + 4.5 + 5.6 + ... + n(n + 1)
(1.1 + 1) + (2.2 + 2) + (3.3 + 3) + ... + (n.n + n)
Ordenando os termos:
1² + 2² + 3² + ... + n² + 1 + 2 + 3 + ... + n
Os termos conhecidos podem ser somados:


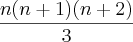
-

Guill
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Dom Jul 03, 2011 17:21
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Cleyson007 » Sex Abr 13, 2012 16:17
por Cleyson007 » Sex Abr 13, 2012 16:17
Boa tarde Guill!
Muito obrigado pela resolução, entendi perfeitamente

Na verdade, eu estava com dúvida na montagem de S
n+1.
Para mim, o outro método é importante em função de conhecimento dado que em minha prova terei que provar utilizando indução.
Mais uma vez, obrigado!
Atenciosamente,
Cleyson007.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Duvida em provar por Indução
por carlosecc » Sáb Dez 08, 2012 21:53
- 3 Respostas
- 2152 Exibições
- Última mensagem por carlosecc

Dom Dez 09, 2012 20:39
Teoria dos Números
-
- Provar igualdade sem recorrer à Indução Matemática
 por EREGON » Ter Abr 14, 2015 06:29
por EREGON » Ter Abr 14, 2015 06:29
- 2 Respostas
- 4071 Exibições
- Última mensagem por e8group

Sex Abr 17, 2015 23:12
Binômio de Newton
-
- [Somatório] Provar pelo Método de Indução Matemática
por Prof Prevaricador » Dom Abr 14, 2013 16:25
- 2 Respostas
- 5070 Exibições
- Última mensagem por Prof Prevaricador

Dom Abr 14, 2013 18:35
Sequências
-
- [hipótese da indução] Indução matemática
por leonardoandra » Sáb Out 12, 2013 22:58
- 1 Respostas
- 2683 Exibições
- Última mensagem por leonardoandra

Seg Out 14, 2013 20:10
Equações
-
- Provar se é par
por stalone » Seg Dez 21, 2009 23:29
- 5 Respostas
- 3224 Exibições
- Última mensagem por stalone

Seg Dez 13, 2010 13:07
Desafios Difíceis
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




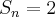 -----> Verdadeiro
-----> Verdadeiro



 ----> Verdade
----> Verdade


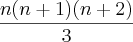




 .
.



