Não estou entendendo essa questão!!!

por **LuizCarlos** » Qua Abr 11, 2012 16:50

Olá amigos,

não estou entendendo essa questão.

A figura tem as seguintes medidas: 25,5cm

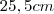de altura, 15cm

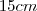de profundidade e 13,5cm

.

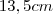Paula tem 1,53m

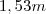. Se ela estivesse nessa foto, qual seria a altura dela na foto.

Tentei resolver sa seguinte maneira: sabendo que

.

Mas a resposta do livro é 42cm

, não estou entendendo.

por **fraol** » Qua Abr 11, 2012 20:54

Presumo que essa seja uma questão de escala, ou melhor, de proporcionalidade.

Assim, se chamarmos de

a altura da figura no livro, é necessário medir lá, e

a medida da Paula na escala da figura, então:

$\frac{x}{153} = \frac{h}{25,5}$ , daí em diante é fazer as contas para achar o valor de

em cm.

por **LuizCarlos** » Qui Abr 12, 2012 14:51

fraol escreveu:Presumo que essa seja uma questão de escala, ou melhor, de proporcionalidade.

Assim, se chamarmos de a altura da figura no livro, é necessário medir lá, e a medida da Paula na escala da figura, então:

$\frac{x}{153} = \frac{h}{25,5}$ , daí em diante é fazer as contas para achar o valor de em cm.

Olá amigo, fraol, é exatamente escala e proporcionalidade! consegui resolver, medi a figura no desenho, e fiz os cálculos!
Consegui obter o mesmo resultado do livro! obrigado.