Por favor me ajudem!! Segue as questões...
1-)Se na expressão
![\frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3} \frac{\left(x-8 \right)}{\sqrt[]{\left(7 + \sqrt[3]{x} \right)}-3}](/latexrender/pictures/5777bacbd014308102cfb07be412cdfa.png) , com x >8, substituirmos
, com x >8, substituirmos ![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) por t, obteremos a expressão equivalente a:
por t, obteremos a expressão equivalente a:a)
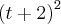
b)
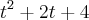
c)
![\sqrt[]{\left(7 + t \right)}+ 3 \sqrt[]{\left(7 + t \right)}+ 3](/latexrender/pictures/8fc2349a2deb23789c73b4d03c38c21c.png)
d)
![\frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}} \frac{{t}^{3} - 8}{\sqrt[]{7} + \sqrt[]{\left(t - 3 \right)}}](/latexrender/pictures/abd3efc8de75ff4a1306fbe4ac51395a.png)
e)
![\left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right] \left({t}^{2} + 2t + 4 \right)\left[\sqrt[]{\left(7 + t \right)} + 3 \right]](/latexrender/pictures/e1a3e00fc17f7bbe10b71827119cdc5b.png)
Resp: E
Eu troquei
![\sqrt[3]{x} \sqrt[3]{x}](/latexrender/pictures/6833f4eaccfb60d5c13fdf6b6cc30aef.png) por t e Racionalizei o denominador ficando...
por t e Racionalizei o denominador ficando...![\frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3} \frac{{t}^{3}-8}{\sqrt[]{7 + t} - 3} \frac{\sqrt[]{7 + t} + 3}{\sqrt[]{7 + t} + 3}](/latexrender/pictures/d307d8081997b5dd52db5dd2d91cff6e.png)
![\frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2} \frac{\left({t}^{3}- 8 \right) \left(\sqrt[]{7 + t} \right) + 3{t}^{3} - 24}{t-2}](/latexrender/pictures/39ed4e4951805ba41b5701959bde6021.png)
Daí em diante não sei mas como fazer =/
Me ajude por favor! =/


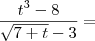
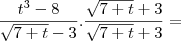
![\frac{(t - 2)(t^2 + 2t + 4)[\sqrt{7 + t} + 3]}{(7 + t) - 9} = \frac{(t - 2)(t^2 + 2t + 4)[\sqrt{7 + t} + 3]}{(7 + t) - 9} =](/latexrender/pictures/cebb8accb70176d897f3ba2ec2100186.png)
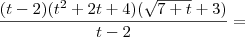
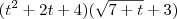


 .
.
 :
: