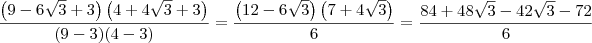1 -
![\frac{4}{\sqrt[]{7}-\sqrt[]{3}}+\sqrt[]{3}-\sqrt[]{7} \frac{4}{\sqrt[]{7}-\sqrt[]{3}}+\sqrt[]{3}-\sqrt[]{7}](/latexrender/pictures/0c2b9cd3151f0d2aea736e3994cb3ddf.png)
Tentei fazer
![\frac{4}{\sqrt[]{7}-\sqrt[]{3}}.\frac{\sqrt[]{7}+\sqrt[]{3}}{\sqrt[]{7}+\sqrt[]{3}} \frac{4}{\sqrt[]{7}-\sqrt[]{3}}.\frac{\sqrt[]{7}+\sqrt[]{3}}{\sqrt[]{7}+\sqrt[]{3}}](/latexrender/pictures/74dfe0b6397850dcfdbaecd8516fb9e5.png) e com o resultado disto eu coloco
e com o resultado disto eu coloco ![\sqrt[]{3}-\sqrt[]{7} \sqrt[]{3}-\sqrt[]{7}](/latexrender/pictures/3823e0dca5e1c278907892938ea19898.png)
A resposta pelo gabarito é :
![2\sqrt[]{3} 2\sqrt[]{3}](/latexrender/pictures/134de3669f0ec101173af9b117543fcd.png)
2 -
![\frac{1}{\sqrt[]{2}}+\frac{1}{\sqrt[]{18}}-\frac{1}{\sqrt[]{8}} \frac{1}{\sqrt[]{2}}+\frac{1}{\sqrt[]{18}}-\frac{1}{\sqrt[]{8}}](/latexrender/pictures/aba5b3da5c4c0a4f1ea37fe08724a42b.png)
Tentei transformar em uma diferença de quadrados
![\frac{1+1-1}{(\sqrt[]{2}+\sqrt[]{18})-\sqrt[]{8}} \frac{1+1-1}{(\sqrt[]{2}+\sqrt[]{18})-\sqrt[]{8}}](/latexrender/pictures/43a5c32efa52b2d1c43c321c05fdecc2.png) .
.![\frac{(\sqrt[]{2}+\sqrt[]{18})+\sqrt[]{8}}{(\sqrt[]{2}+\sqrt[]{18})+\sqrt[]{8}} \frac{(\sqrt[]{2}+\sqrt[]{18})+\sqrt[]{8}}{(\sqrt[]{2}+\sqrt[]{18})+\sqrt[]{8}}](/latexrender/pictures/96042d2b6c76163f432e8972391e4a86.png)
Não deu

Resposta :
![\frac{5\sqrt[]{2}}{12} \frac{5\sqrt[]{2}}{12}](/latexrender/pictures/f6090059774605b1255e2edaa6a510f1.png)
3 -
![\frac{3\sqrt[]{5}+\sqrt[]{2}}{\sqrt[]{5}-\sqrt[]{2}}-2\sqrt[]{10} \frac{3\sqrt[]{5}+\sqrt[]{2}}{\sqrt[]{5}-\sqrt[]{2}}-2\sqrt[]{10}](/latexrender/pictures/99860bb024a106b703264e18b690b88b.png)
Aqui eu tbm tentei fazer a mesma coisa, transformando o denominador numa diferença de quadrados mas não deu certo.
Resposta :
![\frac{17-2\sqrt[]{10}}{3} \frac{17-2\sqrt[]{10}}{3}](/latexrender/pictures/193939fdcce228eb2df8f72c0b1b8576.png)
Bom e mais uma continha aqui que não é pra simplificar mas eu gostaria que me explicassem como fazer pois tenho dificuldade quando se trata de radicais+frações
![\frac{3-\sqrt[]{3}}{3+\sqrt[]{3}} : \frac{2-\sqrt[]{3}}{2+\sqrt[]{3}} \frac{3-\sqrt[]{3}}{3+\sqrt[]{3}} : \frac{2-\sqrt[]{3}}{2+\sqrt[]{3}}](/latexrender/pictures/abc6bb06cade18fc11b86d22fe7f6799.png)
Resposta :
![2+\sqrt[]{3} 2+\sqrt[]{3}](/latexrender/pictures/c683bd721a2ec3c1e6640c0c588b57ae.png)





![\frac{4}{\sqrt{7}-\sqrt[]{3}}+\sqrt{3}-\sqrt{7} \frac{4}{\sqrt{7}-\sqrt[]{3}}+\sqrt{3}-\sqrt{7}](/latexrender/pictures/b5c90efa1f43172ce2a6afb89a481cb2.png)
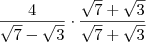 e com o resultado disto eu coloco
e com o resultado disto eu coloco 
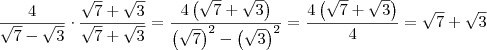
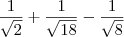
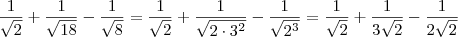
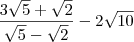
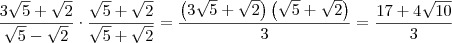
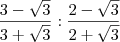
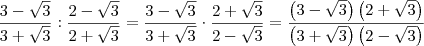
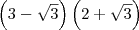 .
.![\frac{\left(3-\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\cdot \frac{\left(3-\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(3-\sqrt{3}\right)\left(2+\sqrt{3}\right)} = \frac{\left(3-\sqrt{3}\right)^2\left(2+\sqrt{3}\right)^2}{\left[3^2-\left(\sqrt{3}\right)^2\right]\left[2^2-\left(\sqrt{3}\right)^2\right]} \frac{\left(3-\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(3+\sqrt{3}\right)\left(2-\sqrt{3}\right)}\cdot \frac{\left(3-\sqrt{3}\right)\left(2+\sqrt{3}\right)}{\left(3-\sqrt{3}\right)\left(2+\sqrt{3}\right)} = \frac{\left(3-\sqrt{3}\right)^2\left(2+\sqrt{3}\right)^2}{\left[3^2-\left(\sqrt{3}\right)^2\right]\left[2^2-\left(\sqrt{3}\right)^2\right]}](/latexrender/pictures/a0a1d207f98a8aa0b11870c53b373ef3.png)

![\frac{(9-6\sqrt[]{3}+3)(4+4\sqrt[]{3}+3)}{((9-3)(4-3)} \frac{(9-6\sqrt[]{3}+3)(4+4\sqrt[]{3}+3)}{((9-3)(4-3)}](/latexrender/pictures/625aa85bf2540cf0ab1df2e0279d1c0f.png) (quadrado da soma e diferença no numerador e diferença de quadrados no denominador) Tentei aplicar a distributiva disto só que o resultado não bateu.
(quadrado da soma e diferença no numerador e diferença de quadrados no denominador) Tentei aplicar a distributiva disto só que o resultado não bateu.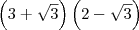 .
.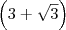 , então precisaríamos multiplicar (numerador e denominador) por
, então precisaríamos multiplicar (numerador e denominador) por 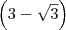 .
.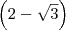 , então precisaríamos multiplicar (numerador e denominador) por
, então precisaríamos multiplicar (numerador e denominador) por 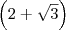 .
.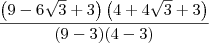 (quadrado da soma e diferença no numerador e diferença de quadrados no denominador) Tentei aplicar a distributiva disto só que o resultado não bateu.
(quadrado da soma e diferença no numerador e diferença de quadrados no denominador) Tentei aplicar a distributiva disto só que o resultado não bateu.