joserd escreveu:Se a+b+c=0 então
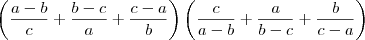
.
Desenvolvendo cada fator, obtemos que:
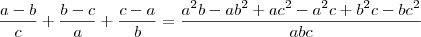

Note que o numerador do primeiro fator é simétrico ao denominador do segundo fator. Desse modo, ao efetuar a multiplicação ficamos apenas com:

Por hipótese, temos que a + b + c = 0.
Multiplicando essa equação por ab, obtemos que:
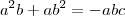
Já se multiplicarmos por bc, obtemos que:
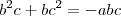
Por fim, se multiplicarmos por ac, obtemos que:

Somando-se essas três relações, obtemos que:
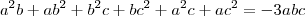
Usando essa informação, podemos reescrever o resultado da multiplicação que encontramos anteriormente:
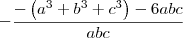
Usando novamente a hipótese, podemos afirmar que

. Desenvolvendo essa equação, obtemos que:
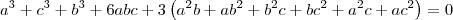
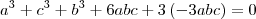

Usando essa informação, podemos reescrever o resultado da multiplicação que encontramos anteriormente:

Realizando as simplificações, obtemos por fim o valor 9.
 .
.
 .
.


 , parece que não resolve pois também vale 0.
, parece que não resolve pois também vale 0.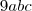 e também parece que não é o caso.
e também parece que não é o caso.

.
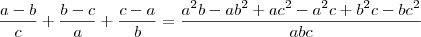


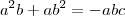
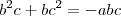

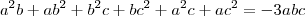
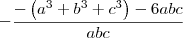
 . Desenvolvendo essa equação, obtemos que:
. Desenvolvendo essa equação, obtemos que: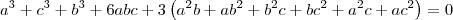
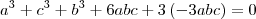




 .
.
 :
: