bom, corrija-me se se eu tiver entendido errado sua expressão... mas estamos falando de
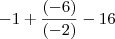
se essa for a expressão você fez tudo direitinho... o erro está na penultima passagem, observe
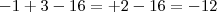
voce fez a conta como se esse 3 fosse negativo também =) um erro completamente compreensível, uma distração.
Agora, quanto a ultima passagem... Sabemos que está errada por causa do -4, tudo bem... mas além disso, voce fez
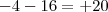
o certo deveria ser -20...
ao subtrair uma quantia de um numero já negativo, voce SEMPRE obterá um numero negativo... não vou insistir nisso, mas se esse erro não foi um erro de pura distração, se por acaso não estiver claríssimo para voce as propriedades algébricas, avise-me!
=D


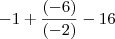
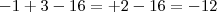
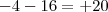



 .
.



