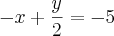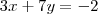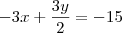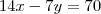por LuizCarlos » Seg Ago 15, 2011 18:16
por LuizCarlos » Seg Ago 15, 2011 18:16
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por LuizCarlos » Seg Ago 15, 2011 18:17
por LuizCarlos » Seg Ago 15, 2011 18:17
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Molina » Seg Ago 15, 2011 21:46
por Molina » Seg Ago 15, 2011 21:46
Luiz Carlos, coloque o enunciado inteiro para que alguém possa te ajudar.
Da forma que você colocou não dá para saber de onde você partiu e onde quer chegar.
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por Caradoc » Seg Ago 15, 2011 22:12
por Caradoc » Seg Ago 15, 2011 22:12
O resultado está certo, mas veja que você deu muita volta até chegar na resposta.
A estratégia no método da adição é tentar somar de modo que uma variável se cancele.
Do jeito que você fez, você apenas somou as duas equações e depois isolou uma das variáveis e substituiu na outra equação.
Se fosse para fazer por substituição, como você tem que x = -y então seria válido substituir o x multiplicando na primeira equação, por -y.
Assim:
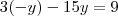
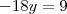
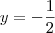
Já para fazer o método da adição, você teria que multiplicar uma das equações (ou as duas) de modo conveniente para cancelar uma variável.
Por exemplo, poderiamos multiplicar a segunda equação por -3 e somar as equações:
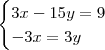
O x cancelaria e ficaríamos com:

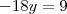

-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizCarlos » Ter Ago 16, 2011 00:17
por LuizCarlos » Ter Ago 16, 2011 00:17
Caradoc escreveu:O resultado está certo, mas veja que você deu muita volta até chegar na resposta.
A estratégia no método da adição é tentar somar de modo que uma variável se cancele.
Do jeito que você fez, você apenas somou as duas equações e depois isolou uma das variáveis e substituiu na outra equação.
Se fosse para fazer por substituição, como você tem que x = -y então seria válido substituir o x multiplicando na primeira equação, por -y.
Assim:
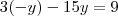
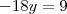

Já para fazer o método da adição, você teria que multiplicar uma das equações (ou as duas) de modo conveniente para cancelar uma variável.
Por exemplo, poderiamos multiplicar a segunda equação por -3 e somar as equações:
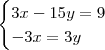
O x cancelaria e ficaríamos com:

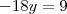

Ola Caradoc, obrigado por me ajudar !
Essa parte do método da substituição eu entendi ! porem o método da adição que você explicou, não consegui entender!
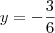
Entendi que você multiplica a segunda equação por
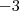
, ficando

Entendi que foi feito a adição
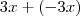
que no caso resultando Zero !
Não entendi a parte do

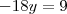
Pra mim ficaria assim
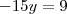
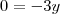
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Caradoc » Ter Ago 16, 2011 10:31
por Caradoc » Ter Ago 16, 2011 10:31
Para manter a igualdade, temos que somar em ambos os lados da equação a mesma quantia.
Eu somei o -3x do lado esquerdo da primeira equação e somei o 3y no lado direito da primeira equação.
Como na segunda equação -3x = 3y, o que eu fiz foi válido, pois apenas somei de cada lado da equação um mesmo valor, não alterando a igualdade.
A soma das equações seria assim:

Você pode pensar da mesma forma que faz uma soma com números, passe um risco em baixo das duas equações, coloque um sinal de igual alinhado e some tudo que está antes do igual nas 2 equações e todo que está depois.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizCarlos » Ter Ago 16, 2011 12:53
por LuizCarlos » Ter Ago 16, 2011 12:53
Caradoc escreveu:Para manter a igualdade, temos que somar em ambos os lados da equação a mesma quantia.
Eu somei o -3x do lado esquerdo da primeira equação e somei o 3y no lado direito da primeira equação.
Como na segunda equação -3x = 3y, o que eu fiz foi válido, pois apenas somei de cada lado da equação um mesmo valor, não alterando a igualdade.
A soma das equações seria assim:

Você pode pensar da mesma forma que faz uma soma com números, passe um risco em baixo das duas equações, coloque um sinal de igual alinhado e some tudo que está antes do igual nas 2 equações e todo que está depois.
Ola amigo, Caradoc, entendi agora, porem estou em duvida somente agora na questão, de olhar as duas equações e saber, por qual número eu devo multiplicar!
Por exemplo, nesse sistema ae, você de cara ja observou que multiplicando a segunda equação por
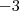
o x ficaria
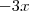
que iria cancelar com o

da primeira equação
Eu tenho dificuldades em observar isso, por exemplo esse sistema aqui !
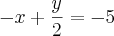
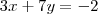
como ficaria pelo método da adição, de forma resumida, para eu não precisar fazer aquela conta gigante que eu faço !
-
LuizCarlos
- Colaborador Voluntário

-
- Mensagens: 254
- Registrado em: Ter Jun 21, 2011 20:39
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: 1º ano do segundo grau
- Andamento: cursando
 por Caradoc » Ter Ago 16, 2011 14:59
por Caradoc » Ter Ago 16, 2011 14:59
Sempre tem vários jeitos de ajeitar o sistema de modo conveniente.
Com a prática você vai pegando qual a operação mais fácil.
Neste segundo caso eu multiplicaria toda a primeira equação por 3, ficando:
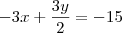
Que somando com a segunda iria eliminar o x.
Mas note que eu também poderia fazer de um modo diferente, multiplicando por exemplo a primeira equação por -14:
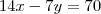
Nesse caso ao somar com a segunda equação eu eliminaria a variável y.
Você pode multiplicar a equação inteira por qualquer número, seja ele positivo, negativo ou uma fração. A estratégia é sempre tentar eliminar uma variável.
-
Caradoc
- Usuário Dedicado

-
- Mensagens: 37
- Registrado em: Qui Dez 16, 2010 17:17
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Sistema Linear] MACK-SP: Sistema de Equações
por ALF » Sex Ago 26, 2011 13:24
- 1 Respostas
- 4489 Exibições
- Última mensagem por LuizAquino

Dom Ago 28, 2011 12:57
Sistemas de Equações
-
- Sistema de equações
por Cleyson007 » Sex Set 12, 2008 12:47
- 6 Respostas
- 5527 Exibições
- Última mensagem por Cleyson007

Qua Jun 03, 2009 17:25
Sistemas de Equações
-
- Sistema de Equações
por Cleyson007 » Qua Mai 27, 2009 14:01
- 3 Respostas
- 3342 Exibições
- Última mensagem por Cleyson007

Qui Mai 28, 2009 17:51
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Seg Mai 17, 2010 15:04
- 3 Respostas
- 3585 Exibições
- Última mensagem por Neperiano

Ter Mai 18, 2010 17:54
Sistemas de Equações
-
- Sistema de equações
por Moreno1986 » Sex Abr 23, 2010 13:54
- 1 Respostas
- 1552 Exibições
- Última mensagem por MarceloFantini

Sáb Abr 24, 2010 00:56
Sistemas de Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
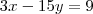
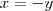
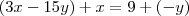

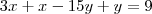
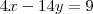
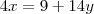
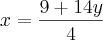
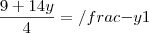
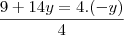
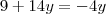
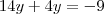

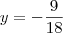

 ?
?
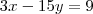
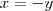
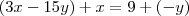

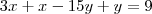
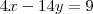
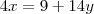
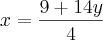
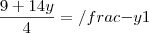
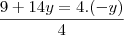
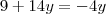
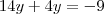

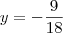


 ?
?
?


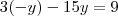
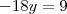

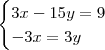

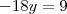


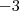 , ficando
, ficando 
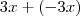 que no caso resultando Zero !
que no caso resultando Zero !
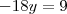
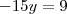
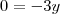



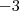
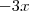
 da primeira equação
da primeira equação