por gustavoluiss » Sex Jul 22, 2011 23:18
Porque 1 - x / x - 1 é igual a -1.
Alguém me explica ??? qual procedimento para fazer essa divisão.
-
gustavoluiss
- Colaborador Voluntário
-
- Mensagens: 118
- Registrado em: Ter Nov 23, 2010 15:59
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Produção
- Andamento: cursando
por m0x0 » Sáb Jul 23, 2011 20:27
É uma questão alterares o sinal:
-
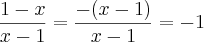
m0x0
- Usuário Ativo
-
- Mensagens: 20
- Registrado em: Qui Jul 21, 2011 15:54
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Álgebra simples
por Rafael16 » Seg Ago 06, 2012 13:45
- 1 Respostas
- 888 Exibições
- Última mensagem por MarceloFantini
Seg Ago 06, 2012 14:56
Álgebra Elementar
-
- Exercícios sobre Juros Simples
por Lote14 » Sáb Set 26, 2015 10:44
- 4 Respostas
- 19073 Exibições
- Última mensagem por nakagumahissao
Ter Nov 28, 2017 05:53
Matemática Financeira
-
- Duvidas sobre equação trigonométrica simples
por Nana_3000 » Sex Dez 23, 2011 10:09
- 7 Respostas
- 4808 Exibições
- Última mensagem por Nana_3000
Sáb Dez 24, 2011 00:38
Trigonometria
-
- Livro sobre Álgebra I
por Caeros » Seg Mar 21, 2011 00:38
- 7 Respostas
- 8267 Exibições
- Última mensagem por Diofanto
Qui Jan 31, 2013 21:21
Álgebra I para Licenciatura
-
- Questão aparentemente simples sobre área do paralelepípedo
por Burna Gioia » Dom Mai 17, 2015 21:10
- 1 Respostas
- 2967 Exibições
- Última mensagem por nakagumahissao
Ter Out 06, 2015 10:41
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
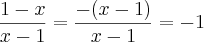
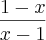
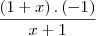
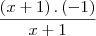
![\frac{1-x}{x-1} = \frac{(-1)\cdot (-1) + x\cdot \left(-1 \right)}{x-1} = \frac{[(-1) + x]\cdot (-1)}{x-1} = \frac{(x - 1)\cdot (-1)}{x-1} = -1](/latexrender/pictures/9ed328a9da1b59c07ee8a707eeebe540.png "\frac{1-x}{x-1} = \frac{(-1)\cdot (-1) + x\cdot \left(-1 \right)}{x-1} = \frac{[(-1) + x]\cdot (-1)}{x-1} = \frac{(x - 1)\cdot (-1)}{x-1} = -1")
