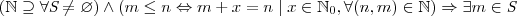
Escrevi corretamente? O que vcs entendem por isso?
Posso utilizar o "e" lógico (
 ) desta forma?
) desta forma?O que vcs sugerem para que eu possa definir que para todo conjunto não vazio pertencente ao conjunto dos numeros naturais existe um elemento minimo?

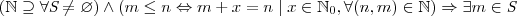
 ) desta forma?
) desta forma?
luiz syncode escreveu:Peço ajuda aos amigos daqui do forum para me ajudar com isto:
Escrevi corretamente?
luiz syncode escreveu:O que vcs entendem por isso?
 contém ou é igual para todo S não vazio e
contém ou é igual para todo S não vazio e  se, e somente se, m + x = n, com x pertencente a
se, e somente se, m + x = n, com x pertencente a 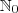 , para todo (n, m) pertencentes a
, para todo (n, m) pertencentes a  , então existe m pertencente a S".
, então existe m pertencente a S".luiz syncode escreveu:Posso utilizar o "e" lógico () desta forma?
luiz syncode escreveu:O que vcs sugerem para que eu possa definir que para todo conjunto não vazio pertencente ao conjunto dos numeros naturais existe um elemento minimo?
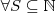 , com
, com 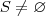 ,
,  tal que
tal que  ,
, 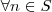 .
.


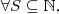 com
com 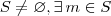 tal que
tal que 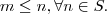
 ser verdadeiro, devemos ter que
ser verdadeiro, devemos ter que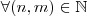
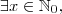 tal que
tal que 

luiz syncode escreveu:Eu também acho muito complicado escrever simbolicamente e também acho que todos os textos que encontro sobre matemática poderiam ter expressões simbólicas, desde que ninguem se esquecesse de "traduzi-las" para o portugues. Mas como isso não acontece, sou obrigado a aprender muito bem a simbologia matemática para entender os textos com os quais tenho me deparado.
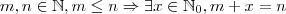 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.