 por igorcamilo » Sáb Jun 25, 2011 21:22
por igorcamilo » Sáb Jun 25, 2011 21:22
o mmc e o mdc entre os números naturais a, x e b, são respectivamente iguais a1680 e 120. Sendo a < x < b , quantos são os valores de x que satisfação essas condições?
a) Nenhuma
b) apenas um.
c) apenas dois
d) apenas três
e) apenas quatro
-
igorcamilo
- Novo Usuário

-
- Mensagens: 6
- Registrado em: Sáb Jun 04, 2011 19:47
- Formação Escolar: ENSINO MÉDIO
- Área/Curso: matemática
- Andamento: cursando
 por FilipeCaceres » Dom Jun 26, 2011 16:13
por FilipeCaceres » Dom Jun 26, 2011 16:13
Primeiramente vamos decompor em fatores primos,
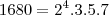
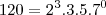
Sabemos que,
O mdc é constituído dos fatores comuns elevados aos menores expoentes.
O mmc é constituído dos fatores comuns elevados aos maiores expoentes.
Assim temos
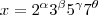
Onde,
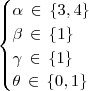
Desta forma o total de possibilidade é
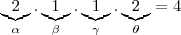
possibilidades.
Mas como

e

devemos subtrair 2, assim
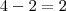
possibilidades.
Resposta
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Colégio Naval
por Joan » Seg Jul 25, 2011 16:38
- 8 Respostas
- 8327 Exibições
- Última mensagem por LuizAquino

Ter Jul 26, 2011 21:35
Álgebra Elementar
-
- Divisibilidade - Colégio naval
por igorcamilo » Sex Jun 24, 2011 19:22
- 2 Respostas
- 2462 Exibições
- Última mensagem por igorcamilo

Sex Jun 24, 2011 20:32
Álgebra Elementar
-
- Colégio Naval - Aritmética dos inteiros
por eliky » Sex Mai 17, 2013 01:16
- 1 Respostas
- 2333 Exibições
- Última mensagem por DanielFerreira

Dom Mai 19, 2013 20:40
Aritmética
-
- [triângulo equilátero] Questão Colégio Naval 2010
 por Joan » Sex Jul 22, 2011 18:42
por Joan » Sex Jul 22, 2011 18:42
- 3 Respostas
- 3722 Exibições
- Última mensagem por Joan

Sáb Jul 23, 2011 11:34
Geometria Plana
-
- [conjunto solução em R] Questão Colégio Naval 2010
por Joan » Sáb Jul 23, 2011 12:06
- 2 Respostas
- 5389 Exibições
- Última mensagem por Joan

Sáb Jul 23, 2011 13:21
Equações
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


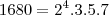
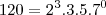
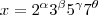
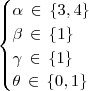
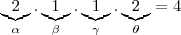 possibilidades.
possibilidades. e
e  devemos subtrair 2, assim
devemos subtrair 2, assim 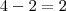 possibilidades.
possibilidades.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.