 por theSinister » Ter Jun 21, 2011 22:04
por theSinister » Ter Jun 21, 2011 22:04
existe uma propriedade da raiz que diz o seguinte :
![\left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}} \left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}}](/latexrender/pictures/3ab38a568fa51bce6f8b2a28e8a1c5d7.png)
, ok?
minha duvida é a seguinte , no caso
![\left(\sqrt[]{a+1} \right){}^{2} \left(\sqrt[]{a+1} \right){}^{2}](/latexrender/pictures/a7f63cd3a1570650d28eb6e5e53e81cf.png)
, eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Claudin » Qua Jun 22, 2011 01:41
por Claudin » Qua Jun 22, 2011 01:41
LuizAquino escreveu:
Vale ressaltar o seguinte: Utilizando a propriedade
![\sqrt[n]{a^m}= a^\frac{m}{n} \sqrt[n]{a^m}= a^\frac{m}{n}](/latexrender/pictures/86d4ba6090aaf3eaca6cf235f488ae05.png)
Portanto:

Por isso logicamente, quando elevamos uma raiz ao quadrado, pode retirar a raiz.
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Jun 22, 2011 09:25
por LuizAquino » Qua Jun 22, 2011 09:25
Claudin escreveu:
Por isso logicamente, quando elevamos uma raiz ao quadrado, pode retirar a raiz.
Tome cuidado!
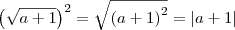
Perceba que não se pode simplesmente "retirar a raiz" e ficar apenas com o radicando.
O que sobra após a simplificação é o módulo do radicando.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por Claudin » Qua Jun 22, 2011 10:19
por Claudin » Qua Jun 22, 2011 10:19
Tome cuidado!
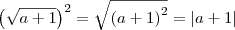
Perceba que não se pode simplesmente "retirar a raiz" e ficar apenas com o radicando.
O que sobra após a simplificação é o módulo do radicando.
Mesmo utilizando a propriedade -->
![\sqrt[n]{a^m}= a^\frac{m}{n} \sqrt[n]{a^m}= a^\frac{m}{n}](/latexrender/pictures/86d4ba6090aaf3eaca6cf235f488ae05.png)
ficaria em módulo? Só ficaria se eu resolvesse extraindo a raiz quadrada não?
"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por theSinister » Qua Jun 22, 2011 11:13
por theSinister » Qua Jun 22, 2011 11:13
vlw , então deixa eu ver se entendi,
não importa se o radicando é uma expressão , se estiver elevado a 2 eu posso tirar ele da raiz, é claro se o indice tbm for 2? certo?
vou aproveitar e tirar outra duvida numa equação do tipo :
![\sqrt[]{5x+3}+\sqrt[]{7x-5}=\sqrt[]{4-2x} \sqrt[]{5x+3}+\sqrt[]{7x-5}=\sqrt[]{4-2x}](/latexrender/pictures/d17962d7dca9ce4bb36aefc77f7b8dc2.png)
ainda to começando a estudar esse assunto e to meio perdido , mas quando é assim , eu elevo os dois menbros da equação ao quadrado? eu vi varias pessoas resolverem dessa forma ,mas não entendi exatamente o pq, quando se tem equações envolvendo radcais qual é a melhor tecnica para resolver?
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Claudin » Qua Jun 22, 2011 11:45
por Claudin » Qua Jun 22, 2011 11:45
Geralmente quando existe uma equação envolvendo raízes quadradas, as pessoas elevam ambos os membros ao quadrado (automaticamente), para que possam "retirar as raízes", se você basear na propriedade que eu mencionei logo em cima da pra compreender. Por exemplo:
![\sqrt[2]{x^1}= \sqrt[2]{16^1}\Rightarrow (x^\frac{1}{2})^2= (16^\frac{1}{2})^2\Rightarrow x^\frac{2}{2}=16^\frac{2}{2}\Rightarrow x=16 \sqrt[2]{x^1}= \sqrt[2]{16^1}\Rightarrow (x^\frac{1}{2})^2= (16^\frac{1}{2})^2\Rightarrow x^\frac{2}{2}=16^\frac{2}{2}\Rightarrow x=16](/latexrender/pictures/f995176041ecae5d1ad8ef85cb21e535.png)
Quando você elevar ambos os membros ao quadrado, utilizando a propriedade, você ficaria com a multiplicação de expoentes que resultaria em 1, falando a grosso modo, "retirando a raíz".

"O que sabemos é uma gota, o que não sabemos é um oceano." - Isaac Newton
-
Claudin
- Colaborador Voluntário

-
- Mensagens: 913
- Registrado em: Qui Mai 12, 2011 17:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por LuizAquino » Qua Jun 22, 2011 12:31
por LuizAquino » Qua Jun 22, 2011 12:31
Claudin escreveu:Mesmo utilizando a propriedade -->
![\sqrt[n]{a^m}= a^\frac{m}{n} \sqrt[n]{a^m}= a^\frac{m}{n}](/latexrender/pictures/86d4ba6090aaf3eaca6cf235f488ae05.png)
ficaria em módulo? Só ficaria se eu resolvesse extraindo a raiz quadrada não?
A regra é:
![\sqrt[n]{x^n} = \begin{cases}|x|,\,\textrm{se } n \textrm{ par;} \\ x,\,\textrm{se } n \textrm{ \'impar;}\end{cases} \sqrt[n]{x^n} = \begin{cases}|x|,\,\textrm{se } n \textrm{ par;} \\ x,\,\textrm{se } n \textrm{ \'impar;}\end{cases}](/latexrender/pictures/a018a371f7320e783c2bebe058a6bc88.png)
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por theSinister » Qua Jun 22, 2011 14:13
por theSinister » Qua Jun 22, 2011 14:13
ah entendi, mas então quando o indice das raizes for 3 por um exemplo, eu elevo os dois lados ao cubo, e assim sucessivamente?essa é a regra? e quando na mesma equação tiver raizes de indices diferentes, o que fazer ?
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por LuizAquino » Qua Jun 22, 2011 15:22
por LuizAquino » Qua Jun 22, 2011 15:22
theSinister escreveu:ah entendi, mas então quando o índice das raízes for 3 por um exemplo, eu elevo os dois lados ao cubo, e assim sucessivamente? essa é a regra?
Basicamente, sim.
theSinister escreveu:e quando na mesma equação tiver raízes de índices diferentes, o que fazer?
Basicamente, você pode primeiro eliminar uma das raízes e depois eliminar a outra.
Por exemplo, digamos que você tenha um radical com índice 2 e outro com índice 3 em uma mesma equação. Você pode primeiro elevar ambos os membros da equação por 2 para eliminar o radical com índice 2. Em seguida, você eleva ambos os membros da equação por 3 para eliminar o radical com índice 3.
Você disse que ainda está começando a estudar esse conteúdo. Não tenha pressa. Provavelmente você ainda estudará essa parte.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por theSinister » Qua Jun 22, 2011 16:16
por theSinister » Qua Jun 22, 2011 16:16
vlw cara , me ajudou muito, a questão é que ja revisei toda a parte de fatoração, peguei uma lista com mais de 50 exercicios e demorei mas consegui resolver rsrsrsr, ja revisei potenciação tbm , mas agora to começando com expressões envolvendo radicais...até agora esta bem facil (uma vez que to aprendendo sozinho pela net) a minha maior dificuldade está sendo quando tem equações com radicais...mas vou continuar firme e as duvidas vou tirando aqui no forum .
vlw e obg.!!!
-
theSinister
- Usuário Dedicado

-
- Mensagens: 41
- Registrado em: Sáb Abr 23, 2011 18:36
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Propriedades da raiz (fácil)
por TAE » Qui Mai 10, 2012 17:39
- 2 Respostas
- 1438 Exibições
- Última mensagem por TAE

Qui Mai 10, 2012 18:25
Álgebra Elementar
-
- [Raiz Cúbica e Raiz Quadrada] Muito difícil achar a solução.
por Leocondeuba » Sáb Mai 11, 2013 19:27
- 2 Respostas
- 7443 Exibições
- Última mensagem por Leocondeuba

Sáb Mai 11, 2013 20:42
Aritmética
-
- Limite - como resolver um lim quando temos raiz^2 e raiz^3.
por Monica santos » Sex Ago 16, 2013 14:22
- 4 Respostas
- 4127 Exibições
- Última mensagem por young_jedi

Sex Ago 16, 2013 19:01
Cálculo: Limites, Derivadas e Integrais
-
- [Limites] Como resolver raiz dentro de raiz ?
 por natyncb » Qui Abr 12, 2012 00:31
por natyncb » Qui Abr 12, 2012 00:31
- 10 Respostas
- 13763 Exibições
- Última mensagem por LuizAquino

Sex Ago 24, 2012 07:50
Cálculo: Limites, Derivadas e Integrais
-
- Cálculo: limite com raiz dentro de raiz
 por roberto_trebor » Sáb Fev 15, 2014 20:45
por roberto_trebor » Sáb Fev 15, 2014 20:45
- 1 Respostas
- 2234 Exibições
- Última mensagem por Man Utd

Dom Fev 16, 2014 17:58
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}} \left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}}](/latexrender/pictures/3ab38a568fa51bce6f8b2a28e8a1c5d7.png) , ok?
, ok?![\left(\sqrt[]{a+1} \right){}^{2} \left(\sqrt[]{a+1} \right){}^{2}](/latexrender/pictures/a7f63cd3a1570650d28eb6e5e53e81cf.png) , eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?
, eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?
![\left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}} \left(\sqrt[n]{a} \right){}^{m}= \sqrt[n]{{a}^{m}}](/latexrender/pictures/3ab38a568fa51bce6f8b2a28e8a1c5d7.png) , ok?
, ok?![\left(\sqrt[]{a+1} \right){}^{2} \left(\sqrt[]{a+1} \right){}^{2}](/latexrender/pictures/a7f63cd3a1570650d28eb6e5e53e81cf.png) , eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?
, eu elevo tudo que esta dentro da raiz ao quadrado ? ou apenas o 1?


![\sqrt[n]{a^m}= a^\frac{m}{n} \sqrt[n]{a^m}= a^\frac{m}{n}](/latexrender/pictures/86d4ba6090aaf3eaca6cf235f488ae05.png)


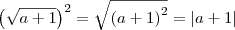

![\sqrt[n]{a^m}= a^\frac{m}{n} \sqrt[n]{a^m}= a^\frac{m}{n}](/latexrender/pictures/86d4ba6090aaf3eaca6cf235f488ae05.png)

![\sqrt[]{5x+3}+\sqrt[]{7x-5}=\sqrt[]{4-2x} \sqrt[]{5x+3}+\sqrt[]{7x-5}=\sqrt[]{4-2x}](/latexrender/pictures/d17962d7dca9ce4bb36aefc77f7b8dc2.png)

![\sqrt[2]{x^1}= \sqrt[2]{16^1}\Rightarrow (x^\frac{1}{2})^2= (16^\frac{1}{2})^2\Rightarrow x^\frac{2}{2}=16^\frac{2}{2}\Rightarrow x=16 \sqrt[2]{x^1}= \sqrt[2]{16^1}\Rightarrow (x^\frac{1}{2})^2= (16^\frac{1}{2})^2\Rightarrow x^\frac{2}{2}=16^\frac{2}{2}\Rightarrow x=16](/latexrender/pictures/f995176041ecae5d1ad8ef85cb21e535.png)


![\sqrt[n]{x^n} = \begin{cases}|x|,\,\textrm{se } n \textrm{ par;} \\ x,\,\textrm{se } n \textrm{ \'impar;}\end{cases} \sqrt[n]{x^n} = \begin{cases}|x|,\,\textrm{se } n \textrm{ par;} \\ x,\,\textrm{se } n \textrm{ \'impar;}\end{cases}](/latexrender/pictures/a018a371f7320e783c2bebe058a6bc88.png)



