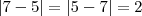por Jorge Rodrigo » Qua Mai 18, 2011 20:41
por Jorge Rodrigo » Qua Mai 18, 2011 20:41
Boa noite!
Meu nome é Jorge Rodrigo e estou cursando duas disciplinas (que ficaram pendentes no meu primeiro período, atualmente estou no segundo, mas cursando ainda essas disciplinas) do primeiro período de matemática na Rural de Nova Iguaçu e gostaria, se possível, que me ajudassem a resolver uma questão da minha lista de exercícios.... ai vai:
![\sqrt[]{{\left[ \frac{1}{2}*\left(\frac{a}{b} \right)^\frac{-1}{2}-\frac{1}{2}*\left\left(\frac{b}{a} \right)^\left(\frac{-1}{2} \right)\right]}^{-2}+1} \sqrt[]{{\left[ \frac{1}{2}*\left(\frac{a}{b} \right)^\frac{-1}{2}-\frac{1}{2}*\left\left(\frac{b}{a} \right)^\left(\frac{-1}{2} \right)\right]}^{-2}+1}](/latexrender/pictures/cc8459cee2bc3bb67e99a95686551072.png)
O gabarito é: a + b/|a - b|.
Abaixo segue minha resolução:
Aplicando propriedades das potências, temos:
![\Rightarrow\sqrt[]{{\left[ \frac{1}{2}*\sqrt[]{\frac{b}{a}} -\frac{1}{2}*\sqrt[]{\frac{a}{b}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[ \frac{1}{2}*\sqrt[]{\frac{b}{a}} -\frac{1}{2}*\sqrt[]{\frac{a}{b}}\right]}^{-2}+1}](/latexrender/pictures/0a448f70a0da879e43e44062446c83d5.png)
Introduzindo um fator no radical, temos:
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}}{\sqrt[]{4a}}-\frac{\sqrt[]{a}}{\sqrt[]{4b}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}}{\sqrt[]{4a}}-\frac{\sqrt[]{a}}{\sqrt[]{4b}}\right]}^{-2}+1}](/latexrender/pictures/f35583abd27a20b0ca20db779c9952d7.png)
Aplicando propriedades da potências, temos:
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{4a}}{\sqrt[]{b}}-\frac{\sqrt[]{4b}}{\sqrt[]{a}}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{4a}}{\sqrt[]{b}}-\frac{\sqrt[]{4b}}{\sqrt[]{a}}\right]}^{2}+1}](/latexrender/pictures/923fd2a2fa263835e1f5ad710cdeb531.png)
Igualando os denominadores, temos:
![\Rightarrow\sqrt[]{{\left[\frac{{2a}}{\sqrt[]{ba}}-\frac{{2b}}{\sqrt[]{ba}}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{{2a}}{\sqrt[]{ba}}-\frac{{2b}}{\sqrt[]{ba}}\right]}^{2}+1}](/latexrender/pictures/de8eaef099f9e9fd692bcdf2bfa46f6b.png)
Aplicando produtos notáveis, temos:
![\Rightarrow\sqrt[]{\frac{{4a}^{2}}{ba}-\frac{8ab}{ba}+\frac{{4b}^{2}}{ba}+1} \Rightarrow\sqrt[]{\frac{{4a}^{2}}{ba}-\frac{8ab}{ba}+\frac{{4b}^{2}}{ba}+1}](/latexrender/pictures/89d6dce4828e46fd8999e688b5863452.png)
Resolvendo a expressão, temos:
![\Rightarrow\sqrt[]{{4a}^{2}-{7ab}+{4b}^{2}} \Rightarrow\sqrt[]{{4a}^{2}-{7ab}+{4b}^{2}}](/latexrender/pictures/a3730019b6598830bcff2ddccb9b28c3.png)
... consegui chegar até aqui!
-
Jorge Rodrigo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 18, 2011 18:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Matemática Aplicada
- Andamento: cursando
 por MarceloFantini » Qua Mai 18, 2011 21:19
por MarceloFantini » Qua Mai 18, 2011 21:19
Errou nas segunda propriedade de potências. Tem que ser uma fração única para aplicar, e não aplicar a cada fração individual. Tente refazer.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Molina » Qua Mai 18, 2011 21:25
por Molina » Qua Mai 18, 2011 21:25
Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por norberto » Qua Mai 18, 2011 21:33
por norberto » Qua Mai 18, 2011 21:33
Oi Jorge :
Você estava até se saindo bem. Mas tem um momento em que você comete um engano muito comum.
O fato de :
![{\left[ \frac{m}{n} \right]}^{-2} {\left[ \frac{m}{n} \right]}^{-2}](/latexrender/pictures/bffe43074b594a2a0bb87ff307038c4a.png)
=
![{\left[ \frac{n}{m} \right]}^{2} {\left[ \frac{n}{m} \right]}^{2}](/latexrender/pictures/04dd5e7bc310f45c15c6247ffcb3ae39.png)
não significa que :
![{\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2} {\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2}](/latexrender/pictures/b5d3156ff01b2a32acb1bb7e52b57918.png)
=
![{\left[ \frac{n}{m} + \frac{p}{o} \right]}^{2} {\left[ \frac{n}{m} + \frac{p}{o} \right]}^{2}](/latexrender/pictures/449af5001ade0d4cb640c2f165c8c4d6.png)
Na verdade, você tem que converter o valor entre colchetes em uma única fração. Neste caso, seria :
(1)
![{\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2} {\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2}](/latexrender/pictures/b5d3156ff01b2a32acb1bb7e52b57918.png)
=
![{\left[ \frac{pm + no}{np} \right]}^{-2} {\left[ \frac{pm + no}{np} \right]}^{-2}](/latexrender/pictures/e6cc80305faed4eb9ebe29c33b6c4073.png)
E agora sim :
(2)
![{\left[ \frac{pm + no}{np} \right]}^{-2} {\left[ \frac{pm + no}{np} \right]}^{-2}](/latexrender/pictures/e6cc80305faed4eb9ebe29c33b6c4073.png)
=
![{\left[ \frac{np}{pm + no} \right]}^{2} {\left[ \frac{np}{pm + no} \right]}^{2}](/latexrender/pictures/7d5143947394da00efac7864b85c2ea3.png)
Creio que você conseguirá desenvolver a questão a partir daí.
Caso contrário, poste suas dúvidas.
-
norberto
- Usuário Dedicado

-
- Mensagens: 33
- Registrado em: Qua Mai 18, 2011 04:38
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
 por Jorge Rodrigo » Sex Mai 20, 2011 02:47
por Jorge Rodrigo » Sex Mai 20, 2011 02:47
Boa noite pessoal!!!!
Primeiramente gostaria de agradecer pelas orientações na resolução da questão. Só permaneceu uma pequena dúvida. O gabarito do livro dá como resultado:
a + b/|a - b| e não a + b/|b - a|. Ou pelo fato de ser módulo a ordem do termos não importa (pois o módulo de um número é sempre positivo: |a| = {a, se a >=0 ou -a, se a<0), ou seja, posso aplicar a propriedade comutativa nesse final?
Desde já, muito obrigado
-
Jorge Rodrigo
- Novo Usuário

-
- Mensagens: 5
- Registrado em: Qua Mai 18, 2011 18:35
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Matemática Aplicada
- Andamento: cursando
 por Molina » Sex Mai 20, 2011 10:29
por Molina » Sex Mai 20, 2011 10:29
Bom dia, Jorge.
Isso mesmo.
Note que, por exemplo,
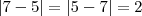

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- POTENCIAÇÃO E RADICIAÇÃO DE RADICAIS
por jacquelinerocha » Ter Mai 10, 2016 15:32
- 2 Respostas
- 2032 Exibições
- Última mensagem por jacquelinerocha

Qui Mai 12, 2016 13:35
Aritmética
-
- [potenciação] raiz cúbica com potenciação
por JKS » Qua Mar 06, 2013 17:41
- 2 Respostas
- 2283 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:43
Álgebra Linear
-
- [potenciação] módulo com potenciação
por JKS » Qua Mar 06, 2013 17:54
- 2 Respostas
- 1730 Exibições
- Última mensagem por JKS

Qui Mar 14, 2013 16:53
Equações
-
- Radicais
por agfp5 » Sáb Out 30, 2010 08:50
- 2 Respostas
- 2333 Exibições
- Última mensagem por agfp5

Sáb Out 30, 2010 09:10
Geometria Plana
-
- Radicais
por Andrewo » Qua Fev 01, 2012 13:43
- 8 Respostas
- 4118 Exibições
- Última mensagem por LuizAquino

Qua Fev 08, 2012 12:22
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Proporcionalidade
Autor:
silvia fillet - Qui Out 13, 2011 22:46
Divida o numero 35 em partes diretamente proporcionais a 4, 10 e 14. Em seguida divida o mesmo numero em partes proporcionais a 6, 15 e 21. explique por que os resultados sao iguais.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Sáb Out 15, 2011 10:25
POR GENTILEZA PODEM VERIFICAR SE O MEU RACIOCINIO ESTÁ CERTO?
P1 = K.4 SUBSTITUINDO K POR 1,25 P1= 5
P2 = K.10 SUBSTITUINDO K POR 1,25 P2= 12,50
P3 = K.13 SUBSTITUINDO K POR 1,25 P3= 17,50
P1+P2+P3 = 35
K.4+K.10+K.13 = 35
28 K = 35
K= 1,25
P1 = K.6 SUBSTITUINDO K POR 0,835 P1= 5
P2 = K.15 SUBSTITUINDO K POR 0,835 P2 = 12,50
P3 = K.21 SUBSTITUINDO K POR 0,835 P3 = 17,50
K.6+K.15+K.21 = 35
42K = 35
K= 0,833
4/6 =10/15 =14/21 RAZÃO = 2/3
SERÁ QUE ESTÁ CERTO?
ALGUEM PODE ME AJUDAR A EXPLICAR MELHOR?
OBRIGADA
SILVIA
Assunto:
Proporcionalidade
Autor:
ivanfx - Dom Out 16, 2011 00:37
utilize a definição e não se baseie no exercícios resolvidos da redefor, assim você terá mais clareza, mas acredito que sua conclusão esteja correto, pois o motivo de darem o mesmo resultado é pq a razão é a mesma.
Assunto:
Proporcionalidade
Autor:
Marcos Roberto - Dom Out 16, 2011 18:24
Silvia:
Acho que o resultado é o mesmo pq as razões dos coeficientes e as razões entre os números são inversamente proporcionais.
Você conseguiu achar o dia em que caiu 15 de novembro de 1889?
Assunto:
Proporcionalidade
Autor:
deiasp - Dom Out 16, 2011 23:45
Ola pessoal
Tb. estou no redefor
O dia da semana em 15 de novembro de 1889, acredito que foi em uma sexta feira
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 06:23
Bom dia,
Realmente foi uma sexta feira, como fazer os calculos para chegar ?
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 07:18
Para encontrar o dia que caiu 15 de novembro de 1889 você deve em primeiro lugar encontrar a quantidade de anos bissextos que houve entre 1889 à 2011, após isso dá uma verificada no ano 1900, ele não é bissexto, pois a regra diz que ano que é múltiplo de 100 e não é múltiplo de 400 não é bissexto.
Depois calcule quantos dias dão de 1889 até 2011, basta pegar a quantidade de anos e multiplicar por 365 + 1 dia a cada ano bissexto (esse resultado você calculou quando encontrou a quantidade de anos bissextos)
Pegue o resultado e divida por 7 e vai obter o resto.
obtendo o resto e partindo da data que pegou como referência conte a quantidade do resto para trás da semana.
Assunto:
Proporcionalidade
Autor:
silvia fillet - Seg Out 17, 2011 07:40
Bom dia,
Será que é assim:
2011 a 1889 são 121 anos sendo , 30 anos bissextos e 91 anos normais então temos:
30x366 = 10.980 dias
91x365 = 33.215 dias
incluindo 15/11/1889 - 31/12/1889 47 dias
33215+10980+47 = 44242 dias
44242:7 = 6320 + resto 2
è assim, nâo sei mais sair disso.
Assunto:
Proporcionalidade
Autor:
ivanfx - Seg Out 17, 2011 10:24
que tal descontar 1 dia do seu resultado, pois 1900 não é bissexto, ai seria 44241 e quando fizer a divisão o resto será 1
como etá pegando base 1/01/2011, se reparar bem 01/01/2011 sempre cai no mesmo dia que 15/01/2011, sendo assim se 01/01/2011 caiu em um sábado volte 1 dia para trás, ou seja, você está no sábado e voltando 1 dia voltará para sexta.então 15/11/1889 cairá em uma sexta
Assunto:
Proporcionalidade
Autor:
Kiwamen2903 - Seg Out 17, 2011 19:43
Boa noite, sou novo por aqui, espero poder aprender e ajudar quando possível! A minha resposta ficou assim:
De 1889 até 2001 temos 29 anos bissextos a começar por 1892 (primeiro múltiplo de 4 após 1889) e terminar por 2008 (último múltiplo de 4 antes de 2011). Vale lembrar que o ano 1900 não é bissexto, uma vez que é múltiplo de 100 mas não é múltiplo de 400.
De um ano normal para outro, se considerarmos a mesma data, eles caem em dias consecutivos da semana. Por exemplo 01/01/2011 – sábado, e 01/01/2010 – sexta.
De um ano bissexto para outro, se considerarmos a mesma data, um cai dois dias da semana depois do outro. Por exemplo 01/01/2008 (ano bissexto) – Terça – feira, e 01/01/09 – Quinta-feira.
Sendo assim, se contarmos um dia da semana de diferença para cada um dos 01/01 dos 122 anos que separam 1889 e 2011 mais os 29 dias a mais referentes aos anos bissextos entre 1889 e 2011, concluímos que são 151 dias da semana de diferença, o que na realidade nos trás: 151:7= 21x7+4, isto é, são 4 dias da semana de diferença. Logo, como 15/11/2011 cairá em uma terça-feira, 15/11/1889 caiu em uma sexta-feira.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\sqrt[]{{\left[ \frac{1}{2}*\left(\frac{a}{b} \right)^\frac{-1}{2}-\frac{1}{2}*\left\left(\frac{b}{a} \right)^\left(\frac{-1}{2} \right)\right]}^{-2}+1} \sqrt[]{{\left[ \frac{1}{2}*\left(\frac{a}{b} \right)^\frac{-1}{2}-\frac{1}{2}*\left\left(\frac{b}{a} \right)^\left(\frac{-1}{2} \right)\right]}^{-2}+1}](/latexrender/pictures/cc8459cee2bc3bb67e99a95686551072.png)
![\Rightarrow\sqrt[]{{\left[ \frac{1}{2}*\sqrt[]{\frac{b}{a}} -\frac{1}{2}*\sqrt[]{\frac{a}{b}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[ \frac{1}{2}*\sqrt[]{\frac{b}{a}} -\frac{1}{2}*\sqrt[]{\frac{a}{b}}\right]}^{-2}+1}](/latexrender/pictures/0a448f70a0da879e43e44062446c83d5.png)
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}}{\sqrt[]{4a}}-\frac{\sqrt[]{a}}{\sqrt[]{4b}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}}{\sqrt[]{4a}}-\frac{\sqrt[]{a}}{\sqrt[]{4b}}\right]}^{-2}+1}](/latexrender/pictures/f35583abd27a20b0ca20db779c9952d7.png)
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{4a}}{\sqrt[]{b}}-\frac{\sqrt[]{4b}}{\sqrt[]{a}}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{4a}}{\sqrt[]{b}}-\frac{\sqrt[]{4b}}{\sqrt[]{a}}\right]}^{2}+1}](/latexrender/pictures/923fd2a2fa263835e1f5ad710cdeb531.png)
![\Rightarrow\sqrt[]{{\left[\frac{{2a}}{\sqrt[]{ba}}-\frac{{2b}}{\sqrt[]{ba}}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{{2a}}{\sqrt[]{ba}}-\frac{{2b}}{\sqrt[]{ba}}\right]}^{2}+1}](/latexrender/pictures/de8eaef099f9e9fd692bcdf2bfa46f6b.png)
![\Rightarrow\sqrt[]{\frac{{4a}^{2}}{ba}-\frac{8ab}{ba}+\frac{{4b}^{2}}{ba}+1} \Rightarrow\sqrt[]{\frac{{4a}^{2}}{ba}-\frac{8ab}{ba}+\frac{{4b}^{2}}{ba}+1}](/latexrender/pictures/89d6dce4828e46fd8999e688b5863452.png)
![\Rightarrow\sqrt[]{{4a}^{2}-{7ab}+{4b}^{2}} \Rightarrow\sqrt[]{{4a}^{2}-{7ab}+{4b}^{2}}](/latexrender/pictures/a3730019b6598830bcff2ddccb9b28c3.png)




![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}*\sqrt{4b}}{\sqrt[]{4a}*\sqrt{4b}}-\frac{\sqrt[]{a}*\sqrt{4a}}{\sqrt[]{4b}*\sqrt{4a}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{b}*\sqrt{4b}}{\sqrt[]{4a}*\sqrt{4b}}-\frac{\sqrt[]{a}*\sqrt{4a}}{\sqrt[]{4b}*\sqrt{4a}}\right]}^{-2}+1}](/latexrender/pictures/0600ec71f29df8558c51516eb857aa79.png)
![\Rightarrow\sqrt[]{{\left[\frac{2 |b|}{\sqrt[]{16ab}}-\frac{2 |a|}{\sqrt{16ab}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{2 |b|}{\sqrt[]{16ab}}-\frac{2 |a|}{\sqrt{16ab}}\right]}^{-2}+1}](/latexrender/pictures/465185daca35990c720e877c88468f43.png)
![\Rightarrow\sqrt[]{{\left[\frac{2 |b| - 2 |a|}{\sqrt[]{16ab}}\right]}^{-2}+1} \Rightarrow\sqrt[]{{\left[\frac{2 |b| - 2 |a|}{\sqrt[]{16ab}}\right]}^{-2}+1}](/latexrender/pictures/6ad42f89b92d4d0ce971df9d37646305.png)
![\Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{16ab}}{2 |b| - 2 |a|}\right]}^{2}+1} \Rightarrow\sqrt[]{{\left[\frac{\sqrt[]{16ab}}{2 |b| - 2 |a|}\right]}^{2}+1}](/latexrender/pictures/4c891548f83c235294929b42ec711696.png)
![\Rightarrow\sqrt[]{{\frac{16ab}{(2 |b| - 2 |a|)^2 }}+1} \Rightarrow\sqrt[]{{\frac{16ab}{(2 |b| - 2 |a|)^2 }}+1}](/latexrender/pictures/56e465f9e25393abb51c94dc1fb7d939.png)
![\Rightarrow\sqrt[]{{\frac{16ab+(2 |b| - 2 |a|)^2}{(2 |b| - 2 |a|)^2 }}} \Rightarrow\sqrt[]{{\frac{16ab+(2 |b| - 2 |a|)^2}{(2 |b| - 2 |a|)^2 }}}](/latexrender/pictures/8a6f5be71e7e3c0030a3cc5b35ea0cee.png)



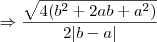

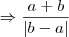

![{\left[ \frac{m}{n} \right]}^{-2} {\left[ \frac{m}{n} \right]}^{-2}](/latexrender/pictures/bffe43074b594a2a0bb87ff307038c4a.png) =
= ![{\left[ \frac{n}{m} \right]}^{2} {\left[ \frac{n}{m} \right]}^{2}](/latexrender/pictures/04dd5e7bc310f45c15c6247ffcb3ae39.png)
![{\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2} {\left[ \frac{m}{n} + \frac{o}{p} \right]}^{-2}](/latexrender/pictures/b5d3156ff01b2a32acb1bb7e52b57918.png) =
= ![{\left[ \frac{n}{m} + \frac{p}{o} \right]}^{2} {\left[ \frac{n}{m} + \frac{p}{o} \right]}^{2}](/latexrender/pictures/449af5001ade0d4cb640c2f165c8c4d6.png)
![{\left[ \frac{pm + no}{np} \right]}^{-2} {\left[ \frac{pm + no}{np} \right]}^{-2}](/latexrender/pictures/e6cc80305faed4eb9ebe29c33b6c4073.png)
![{\left[ \frac{np}{pm + no} \right]}^{2} {\left[ \frac{np}{pm + no} \right]}^{2}](/latexrender/pictures/7d5143947394da00efac7864b85c2ea3.png)