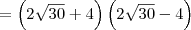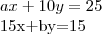
a)Determine os valores de a e b tais que o sistema tenha mais de uma soluçao.
gabarito a=25 b=6
tentei usolar um temo e subistitur na equaçao mais nao sei como cancelo x,y ou as incognitas
(UFF)A confeitaria "cara melada" é conhecida por suas famosas balas de leite, vendidas em pacotes. No Natal,essa confeitaria fez a seguinte promoçao:colocou, em cada pacote,20% a mais de balas e aumentou em 8% o preço do pacote.Determine a variaçao,em porcentagem, que essa promoçao acarretou no preço de cada bala do pacote.
Gabarito Reduçao de 10%
tentei considerar que cada pacote tem 100 balas,logo 20% a mais é 120 balas . mas quando se trata de variaçao da porcentagem tenho duvivas em como montar uma equaçao.
O produto
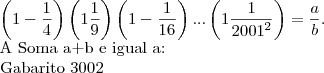
nao encontrei um caminho para resolver este exercicio
(Puc)O produto P=
![\left(\sqrt[]{5}+\sqrt[]{6}+\sqrt[]{7} \right)\left(\sqrt[]{5}+\sqrt[]{6}-\sqrt[]{7} \right)\left(\sqrt[]{5}-\sqrt[]{6}+\sqrt[]{7} \right)\left(-\sqrt[]{5}+\sqrt[]{6}+\sqrt[]{7} \right) \left(\sqrt[]{5}+\sqrt[]{6}+\sqrt[]{7} \right)\left(\sqrt[]{5}+\sqrt[]{6}-\sqrt[]{7} \right)\left(\sqrt[]{5}-\sqrt[]{6}+\sqrt[]{7} \right)\left(-\sqrt[]{5}+\sqrt[]{6}+\sqrt[]{7} \right)](/latexrender/pictures/9e122674ed8291a3d29466361d6603a0.png)
Gabarito 104
tentei colocar todos os termo dentro de uma unica raiz mas ao efetuar a multiplicaçao o resultados nao bate acho que nao estou indo pelo caminho correto


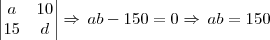
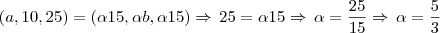
 temos como determinar a e b, veja:
temos como determinar a e b, veja: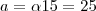
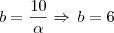
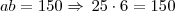
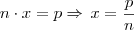
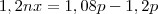
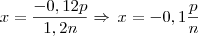
 o preço individual de cada bala, então teremos uma redução de 10% no preço individual de cada bala....
o preço individual de cada bala, então teremos uma redução de 10% no preço individual de cada bala....
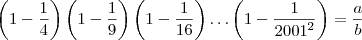 . A Soma a+b e igual a: Gabarito 3002
. A Soma a+b e igual a: Gabarito 3002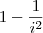 , com
, com 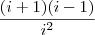 . Portanto o produto é o mesmo que:
. Portanto o produto é o mesmo que: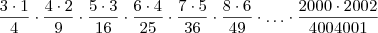
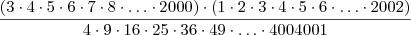
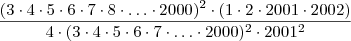
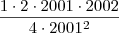
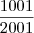



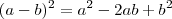
![\left[\left(\sqrt[]{5}+\sqrt[]{6}\right)+\sqrt[]{7} \right]\left[\left(\sqrt[]{5}+\sqrt[]{6}\right)-\sqrt[]{7} \right]\left[\sqrt[]{7} + \left(\sqrt[]{5}-\sqrt[]{6}\right)\right]\left[\sqrt[]{7} -\left(\sqrt[]{5}-\sqrt[]{6}\right)\right] = \left[\left(\sqrt[]{5}+\sqrt[]{6}\right)+\sqrt[]{7} \right]\left[\left(\sqrt[]{5}+\sqrt[]{6}\right)-\sqrt[]{7} \right]\left[\sqrt[]{7} + \left(\sqrt[]{5}-\sqrt[]{6}\right)\right]\left[\sqrt[]{7} -\left(\sqrt[]{5}-\sqrt[]{6}\right)\right] =](/latexrender/pictures/48b2d11e577db6a3a420be6377abb176.png)
![= \left[\left(\sqrt[]{5}+\sqrt[]{6}\right)^2 - \sqrt[]{7}^2 \right]\left[\sqrt[]{7}^2 - \left(\sqrt[]{5}-\sqrt[]{6}\right)^2\right]\right) = \left[\left(\sqrt[]{5}+\sqrt[]{6}\right)^2 - \sqrt[]{7}^2 \right]\left[\sqrt[]{7}^2 - \left(\sqrt[]{5}-\sqrt[]{6}\right)^2\right]\right)](/latexrender/pictures/d605004ee871e3c56f8da20515c4509c.png)