Definições do livro do Castrucci:
Um corpo é um anel com elemento unidade 1, onde todo elemento -{0}(elemento neutro da +) possui inverso.
Um domínio de integridade (ou anel de integridade) é um anel comutativo(vale a comutatividade na segunda operação(1) ) com elemento unidade e não possui divisores próprios do zero(2).
Todo corpo é domínio de integridade. Prova:
Seja C um corpo. Como vale o elemento inverso em C, a.a'=a'.a=1, logo também vale a comutatividade para a segunda operação. (1)
Suponha por absurdo que 0 tem inverso.
0.0'=1
0.0' + 0 = 1 + 0
0.(0' + 0) = 1
0 = 1
Absurdo, já que 0 é diferente de 1, logo 0.0'
 1 ou 0.0' = 0, mas como 0' não existe em C, 0 não tem divisores próprios.(2)
1 ou 0.0' = 0, mas como 0' não existe em C, 0 não tem divisores próprios.(2)Algum perito em teoria dos conjuntos pode corrigir isto pra mim? Grato.


 ,
,  tais que
tais que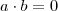 e
e  e
e 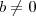

 e
e 
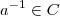 tal que
tal que
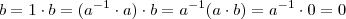
 , então
, então  um anel comutativo com unidade.
um anel comutativo com unidade.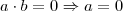

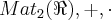 (o conjunto de todas as matrizes reais 2x2). Cuja unidade é:
(o conjunto de todas as matrizes reais 2x2). Cuja unidade é:
 ,
, 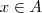 tal que
tal que  ).
). é único e indicado por
é único e indicado por  .
.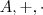 satisfaz a propriedade:
satisfaz a propriedade: tal que
tal que  ,
,![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)