 por johnlaw » Dom Fev 27, 2011 14:14
por johnlaw » Dom Fev 27, 2011 14:14
Olá pessoal,
Não não consigo verificar se está correto ou não se as duas equações estão iguais ou não..
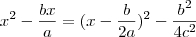
Eu não consigo entender o que foi feito... o porque está errado ou certo..
Se alguém puder me ajudar... ficarei muito grato.
Obrigado desde já.
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por Renato_RJ » Dom Fev 27, 2011 14:38
por Renato_RJ » Dom Fev 27, 2011 14:38
Boa tarde, tudo bem ?
Seguinte, o último termo é
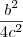
mesmo ?? Pois se fosse

no lugar do
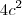
as equações seriam idênticas (é só desenvolver o binômio do termo a direita da igualdade que você verá).
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por johnlaw » Dom Fev 27, 2011 15:25
por johnlaw » Dom Fev 27, 2011 15:25
É mesmo, está errado, o correto é:
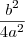
.
Ok, mas como faço isso ?
Obrigado hein!
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por Renato_RJ » Dom Fev 27, 2011 18:54
por Renato_RJ » Dom Fev 27, 2011 18:54
Sem problemas, vamos lá...

Resolvendo, teremos:
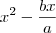
Espero ter ajudado....
Abraços,
Renato.
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
 por johnlaw » Seg Fev 28, 2011 14:24
por johnlaw » Seg Fev 28, 2011 14:24
Aoo Renato...
Agora clareou tudo!! Peguei o que quis dizer com.. desenvolver...
Muito obrigado...
Fique com Deus, um grande abraço.
-
johnlaw
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Ago 06, 2010 13:12
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática Licenciatura
- Andamento: cursando
 por Renato_RJ » Seg Fev 28, 2011 15:12
por Renato_RJ » Seg Fev 28, 2011 15:12
Iniciando a minha "caminhada" pela matemática agora... Tenho muito o quê aprender...
-

Renato_RJ
- Colaborador Voluntário

-
- Mensagens: 306
- Registrado em: Qui Jan 06, 2011 15:47
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado em Matemática
- Andamento: cursando
Voltar para Álgebra Elementar
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Álgebra Elementar
por Abelardo » Seg Mar 14, 2011 18:09
- 1 Respostas
- 2311 Exibições
- Última mensagem por LuizAquino

Seg Mar 14, 2011 18:21
Álgebra Elementar
-
- Álgebra Elementar
por Thiago Josep » Sex Set 05, 2014 15:32
- 1 Respostas
- 2664 Exibições
- Última mensagem por DanielFerreira

Qui Jan 01, 2015 22:22
Álgebra Elementar
-
- Exercicio-Algebra elementar
por Renks » Seg Fev 14, 2011 20:38
- 3 Respostas
- 4727 Exibições
- Última mensagem por Renks

Ter Fev 15, 2011 13:55
Álgebra Elementar
-
- Questão - Álgebra Elementar
por Oliver » Qua Fev 16, 2011 13:10
- 1 Respostas
- 2550 Exibições
- Última mensagem por DanielFerreira

Qui Fev 17, 2011 16:32
Álgebra Elementar
-
- Demonstrações! Álgebra elementar
por Abelardo » Ter Mar 08, 2011 00:42
- 5 Respostas
- 6913 Exibições
- Última mensagem por Abelardo

Ter Mar 08, 2011 14:35
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 3 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
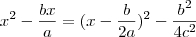

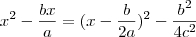

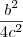 mesmo ?? Pois se fosse
mesmo ?? Pois se fosse  no lugar do
no lugar do 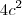 as equações seriam idênticas (é só desenvolver o binômio do termo a direita da igualdade que você verá).
as equações seriam idênticas (é só desenvolver o binômio do termo a direita da igualdade que você verá).
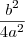 .
.

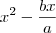




 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
