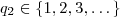Olá
heroncius!
Nesta questão, em primeiro lugar, acho importante
* utilizarmos a seguinte propriedade:

Então, vamos identificar

.
Como:
dividindo-se um número "X" por 5 obtem-se resto 2
Podemos expressar da seguinte forma:

Daqui:
dividindo-se um número "Y" por 5 obtem-se resto 4
Escrevemos:
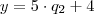
Com
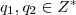
De modo que o produto

será:
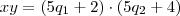
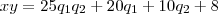 *
*A expansão desta potência
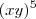
:
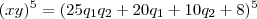
Terá a seguinte
aparência (informalmente):
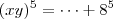
Onde
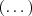
são produtos envolvendo
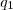
e
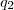
, sendo todos estes produtos múltiplos de 5, porque são múltiplos, ou de 25, ou de 20, ou de 10.
Ou seja, para que

(com

ou

) seja múltiplo de 5, bastará que:
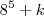
seja múltiplo de 5.
Como pede-se o menor

, e
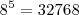
, temos:
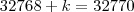
(múltiplo de 5)
Com

.
Alternativa d) k=2heroncius, repare que há infinitas possibilidades para os valores de
x e de
y.
Podem ser obtidos a partir destas equações:

Com
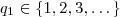
e
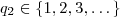
Ou seja,
x pode ser 7, 12, 17, 23 etc.
y pode ser 9, 14, 19, 24 etc.



 .
.
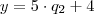
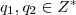
 será:
será: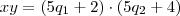
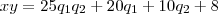
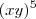 :
: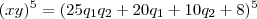
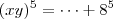
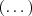 são produtos envolvendo
são produtos envolvendo 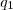 e
e 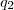 , sendo todos estes produtos múltiplos de 5, porque são múltiplos, ou de 25, ou de 20, ou de 10.
, sendo todos estes produtos múltiplos de 5, porque são múltiplos, ou de 25, ou de 20, ou de 10. (com
(com  ou
ou  ) seja múltiplo de 5, bastará que:
) seja múltiplo de 5, bastará que: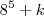 seja múltiplo de 5.
seja múltiplo de 5. , e
, e 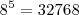 , temos:
, temos: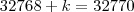 (múltiplo de 5)
(múltiplo de 5) .
.
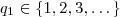 e
e