

então essa é a equação toda , ai eu tirei o mmc tal .E cheguei nesse resultado ...
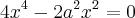

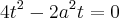
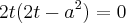

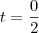

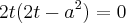
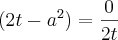




![x" =\frac{\sqrt[]{a^2}}{\sqrt[]{2}} x" =\frac{\sqrt[]{a^2}}{\sqrt[]{2}}](/latexrender/pictures/268fbeec055e3127c7bdf047fb551e6c.png)
![x" =\frac{a}{\sqrt[]{2}} x" =\frac{a}{\sqrt[]{2}}](/latexrender/pictures/c98d836f4b78378f8b4fbb41fd3be458.png)
![x" =\frac{a}{\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}} x" =\frac{a}{\sqrt[]{2}} . \frac{\sqrt[]{2}}{\sqrt[]{2}}](/latexrender/pictures/b62d3f998a2a6dbb466f3aa8cacf7884.png)
![x" =+-\frac{a\sqrt[]{2}}{2} x" =+-\frac{a\sqrt[]{2}}{2}](/latexrender/pictures/d9cae559e10b29997be4d7236194d408.png)
![V=\left(-\frac{a\sqrt[]{2}}{2} ,0,\frac{a\sqrt[]{2}}{2} \right) V=\left(-\frac{a\sqrt[]{2}}{2} ,0,\frac{a\sqrt[]{2}}{2} \right)](/latexrender/pictures/edf05353bee2430f97b85fb6a7edf0ea.png)
bom gente aparentemente parece estar certo tudo isso , mais tem um detale que nao condiz com o gabarito que está ....
![V=\left(-\frac{\sqrt[]{a^2+2}}{2} ,0,\frac{\sqrt[]{a^2+2}}{2} \right) V=\left(-\frac{\sqrt[]{a^2+2}}{2} ,0,\frac{\sqrt[]{a^2+2}}{2} \right)](/latexrender/pictures/90f691bdef4abae3196403ff9eaf163a.png)
POr favor se alguem poder me dizer aondi foi q eu errei, agradeço muito . Pois eu já fiz e refiz essa equação varias vez e não encontrei o erro .



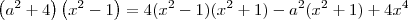

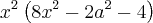
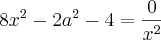

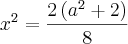
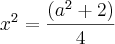
![x=\frac{\left(\sqrt[]{a^2+2 }\right)}{\sqrt[]{4}} x=\frac{\left(\sqrt[]{a^2+2 }\right)}{\sqrt[]{4}}](/latexrender/pictures/e53317be8737cdef3ac5e8c87b2522b7.png)
![x' =+-\frac{\left(\sqrt[]{a^2+2 }\right)}{2} x' =+-\frac{\left(\sqrt[]{a^2+2 }\right)}{2}](/latexrender/pictures/270d27473a3ed3e1db647b0dfd2a29f5.png)



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)