Comentem, corrijam!
M01
Em uma competição de vólei, estão inscritos 5 times.Pelo regulamento, todos os times devem se enfrentar apenas uma vez e, ao final da competição, eles serão classificados pelo número de vitórias. Dois ou mais times com o mesmo número de vitórias terão a mesma classificação. Em cada jogo, os times têm probabilidade
 de vencer.
de vencer.a) Explique por que 2 times não podem empatar na classificação com 4 vitórias cada um
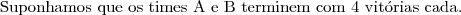

b) Qual é a probabilidade que o primeiro classificado termine a competição com 4 vitórias?
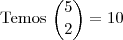







c) Qual é a probabilidade de que os 5 times terminem empatados na classificação?

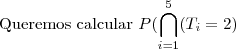
Primeira opção: passar pelo evento complementar. Reduziremos o número de cálculos já que aparecerão eventos incompatíveis (as combinações de
 e
e  )
)

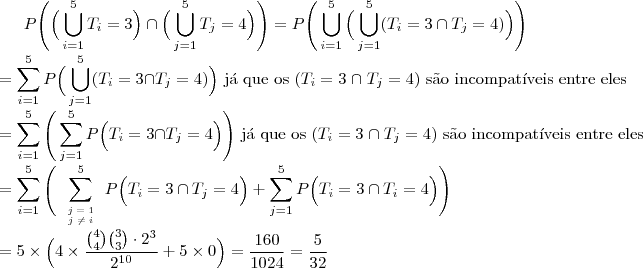
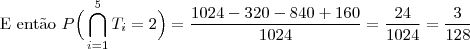
Segunda Opção: usar os resultados possíveis dos jogos de 4 times entre eles
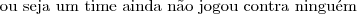



Terceira opção: calcular diretamente
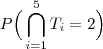

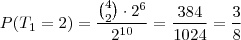

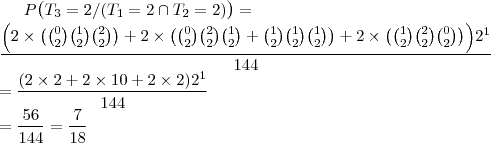
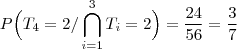
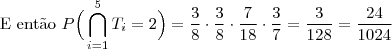
M02
Considere as funções
![f:\;[-\frac{\pi}{2};\frac{\pi}{2}]\rightarrow[-1;1] f:\;[-\frac{\pi}{2};\frac{\pi}{2}]\rightarrow[-1;1]](/latexrender/pictures/75fa245bc12d5cf3cc9b2ce941b79c7e.png) e
e ![g:\;[0;\pi]\rightarrow[-1;1] g:\;[0;\pi]\rightarrow[-1;1]](/latexrender/pictures/74aa2ac182c09f10873a477fd03114ca.png) definidas por
definidas por 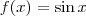 e
e 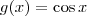 . Sendo f e g bijetoras, existem funções
. Sendo f e g bijetoras, existem funções  e
e  tais que
tais que 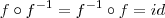 e
e  , em que
, em que 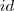 é a função identidade.
é a função identidade.a) Para
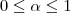 , mostre que
, mostre que 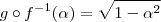
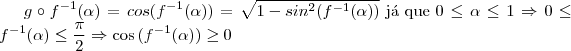
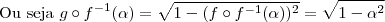

b) Mostre que
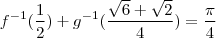
Usar o resultado da primeira questão é um complicação desnecessária quando:
![\begin{array}{rl}f^{-1}(\dfrac{1}{2}) + g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})=&f^{-1}(\sin{\dfrac{\pi}{6}})+g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\dfrac{1}{\sqrt{2}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{\sqrt{2}}\cdot\dfrac{1}{2}\Big )\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\cos{\dfrac{\pi}{4}}\cos{\dfrac{\pi}{6}}+\sin{\dfrac{\pi}{4}}\sin{\dfrac{\pi}{6}\Big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\big (\cos{(\dfrac{\pi}{4}-\dfrac{\pi}{6})}\big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +\dfrac{\pi}{12}\\[\bigskipamount]=&\dfrac{\pi}{4}\end{array} \begin{array}{rl}f^{-1}(\dfrac{1}{2}) + g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})=&f^{-1}(\sin{\dfrac{\pi}{6}})+g^{-1}(\dfrac{\sqrt{6}+\sqrt{2}}{4})\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\dfrac{1}{\sqrt{2}}\cdot\dfrac{\sqrt{3}}{2}+\dfrac{1}{\sqrt{2}}\cdot\dfrac{1}{2}\Big )\\[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\Big(\cos{\dfrac{\pi}{4}}\cos{\dfrac{\pi}{6}}+\sin{\dfrac{\pi}{4}}\sin{\dfrac{\pi}{6}\Big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +g^{-1}\big (\cos{(\dfrac{\pi}{4}-\dfrac{\pi}{6})}\big)\\
[\bigskipamount]=&\dfrac{\pi}{6} +\dfrac{\pi}{12}\\[\bigskipamount]=&\dfrac{\pi}{4}\end{array}](/latexrender/pictures/0ce6dc6b75247a38575eb4802b96af6b.png)
Ou, usando o resultado de a):
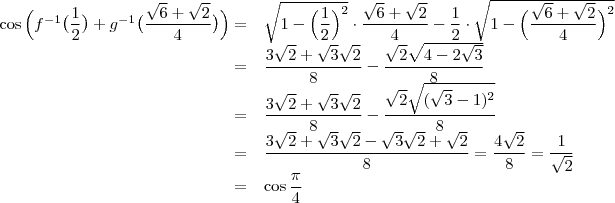
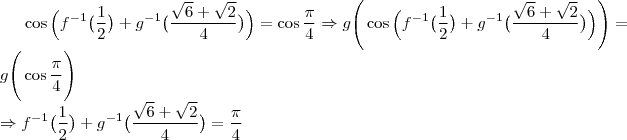
M03
Sejam C um subconjunto não vazio e P um ponto, ambos em um mesmo plano, tais que
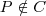 , Diz-se que "P enxerga C sob um ângulo
, Diz-se que "P enxerga C sob um ângulo  se
se  for a medida do menor ângulo com vértice em P que contenha C.
for a medida do menor ângulo com vértice em P que contenha C.a) Se C for um circulo de raio r , centrado na origem de um plano cartesiano real, determine o lugar geométrico dos pontos que enxergam C sob um ângulo de 60 graus
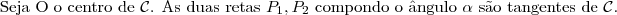

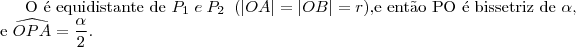
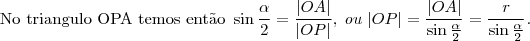

b) Se
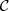 for a união dos segmentos
for a união dos segmentos 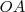 e
e  em que
em que  ,
, 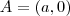 e
e 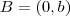 , com
, com 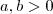 , determine o lugar geométrico dos pontos que enxergam
, determine o lugar geométrico dos pontos que enxergam  sob um ângulo de 90 graus.
sob um ângulo de 90 graus.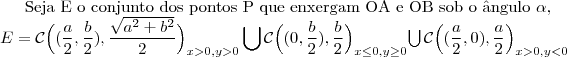
M04
Considere a sequência
 e
e 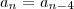 para
para  . Defina
. Defina  para
para 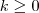 , isto é a soma de (k+1) termos consecutivos da sequência começanco no n-ésimo, por exemplo
, isto é a soma de (k+1) termos consecutivos da sequência começanco no n-ésimo, por exemplo 
a) Encontre
 tais que
tais que 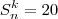

b) Para cada inteiro
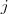 ,
, 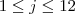 , encontre
, encontre  tais que
tais que 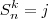

3) Mostre que para qualquer inteiro
 , existem inteiros
, existem inteiros 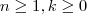 tais que
tais que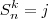


M05
Para responder aos itens a) e b) considere a figura correspondente
a) num tetraedro OABC, os ângulos
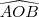 ,
, 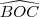 e
e 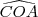 medem 90 graus. Sejam
medem 90 graus. Sejam  e
e  as medidas dos ângulos
as medidas dos ângulos  e
e 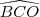 , respetivamente,expresse o cosseno do ângulo
, respetivamente,expresse o cosseno do ângulo 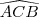 em função de
em função de  e
e 


b) Um navio parte do ponto de latitude 0° e de longitude 0°e navega até chagar ao ponto de latitude 45° sul e longitude 45° oeste, seguindo a trajetória que minimiza a distância percorrida. Admita que a terra seja esférica de raio
 . Qual foi a distância percorrida pelo navio?
. Qual foi a distância percorrida pelo navio?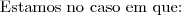
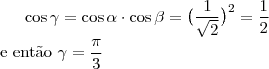
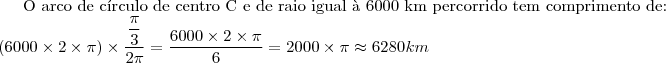
M06
Considere a função real definida por

a) Qual é o domínio de f?
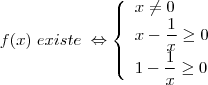
![x-\dfrac{1}{x}\geq 0 \Leftrightarrow \dfrac{x^2-1}{x} \geq 0 \Leftrightarrow \left \{\begin{array}{l}x^2-1\geq 0\;se\;x> 0\\x^2-1\leq 0\;se\;x< 0 \end{array} \right\Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\geq -1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in [-1;0[\cup]1;+\infty[ x-\dfrac{1}{x}\geq 0 \Leftrightarrow \dfrac{x^2-1}{x} \geq 0 \Leftrightarrow \left \{\begin{array}{l}x^2-1\geq 0\;se\;x> 0\\x^2-1\leq 0\;se\;x< 0 \end{array} \right\Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\geq -1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in [-1;0[\cup]1;+\infty[](/latexrender/pictures/8851b70be126d8ae0d70497f53842dc1.png)
![1-\dfrac{1}{x}\geq 0 \Leftrightarrow 1 \geq \dfrac{1}{x} \Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\leq 1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in ]-\infty;0[\cup[1;+\infty[ 1-\dfrac{1}{x}\geq 0 \Leftrightarrow 1 \geq \dfrac{1}{x} \Leftrightarrow \left \{\begin{array}{l}x\geq 1\;se\;x> 0\\x\leq 1\;se\;x< 0 \end{array} \right\Leftrightarrow x\in ]-\infty;0[\cup[1;+\infty[](/latexrender/pictures/42358de9232e9b9d8463403170f86b7b.png)
![\mathcal{D}_f = \mathbb{R}^*\;\; \cap\;\; \big ([-1;0[\cup]1;+\infty[\big )\;\; \cap \;\;\big (]-\infty;0[\cup[1;+\infty[\big )=[-1;0[\cup[1;+\infty[ \mathcal{D}_f = \mathbb{R}^*\;\; \cap\;\; \big ([-1;0[\cup]1;+\infty[\big )\;\; \cap \;\;\big (]-\infty;0[\cup[1;+\infty[\big )=[-1;0[\cup[1;+\infty[](/latexrender/pictures/10f9f7c02f2f3590eba1ab45d14f71ed.png)
b) Encontre o(s) valor(es) de
 para o(s) qual(is)
para o(s) qual(is) 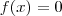
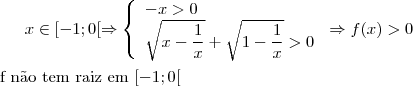

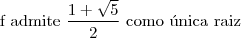



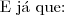
>\dfrac{b^2}{4} \end{array} \right \\[\bigskipamount]&\Rightarrow \big (x-\dfrac{a}{2}\big )^2+\big (y-\dfrac{b}{2}\big )^2>\dfrac{a^2+b^2}{4}\\[\bigskipamount]&\Rightarrow \mathcal{C}\Big((\dfrac{a}{2},\dfrac{b}{2}),\dfrac{\sqrt{a^2+b^2}}{2}\Big)_{x<0,y<0}=\emptyset ,\end{array}\\ \begin{array}{rl} \left \begin{array}{rl}x<0\\y<0 \end{array}\right \} &\Rightarrow \left \{ \begin{array}{rl}(x-\dfrac{a}{2})>\dfrac{a^2}{4}\\[\bigskipamount](y-\dfrac{b}{2})>\dfrac{b^2}{4} \end{array} \right \\[\bigskipamount]&\Rightarrow \big (x-\dfrac{a}{2}\big )^2+\big (y-\dfrac{b}{2}\big )^2>\dfrac{a^2+b^2}{4}\\[\bigskipamount]&\Rightarrow \mathcal{C}\Big((\dfrac{a}{2},\dfrac{b}{2}),\dfrac{\sqrt{a^2+b^2}}{2}\Big)_{x<0,y<0}=\emptyset ,\end{array}\\](/latexrender/pictures/9a0f8b604151253bcffae7ba9e417826.png)

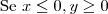
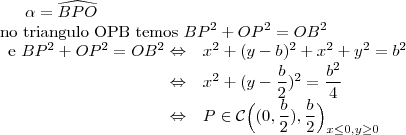



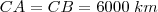
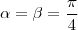

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.