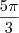Tenho um subespaço de R^4, gerado por 4 vetores S = {(1,2,-1,3) , (3,0,1,-2) , (1,-4,3,-8) , (5,-8,7,-18)}. Esse espaço tem dimensão igual a 2. Faço a matriz A (4x4), cujas colunas são os 4 vetores. Tomamos o sistema A.X = 0, e obtemos como solução geral, X = [(4a + 2b , -3a - b , b , a)]. Escrevo X...


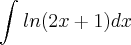
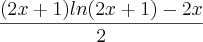
 |a - b|, para todo a e b
|a - b|, para todo a e b [0 , 2
[0 , 2 ] verifica-se a desigualdade:
] verifica-se a desigualdade: +
+  > 1
> 1 < x <
< x <  ou
ou 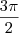 < x <
< x <