Ajuda Matemática • Pesquisar

Avaliei aqui . Seu raciocínio estar parcialmente certo .Vamos começa por aqui . Como vc disse , " Eles disseram que as distâncias entre os pontos onde a bolinha toca o solo são iguais. Se a primeira é 0, e a segunda é 2(as raízes da função), a terceira será 4, o quarto ponto 6 e o último 8 . &...

MarceloFantini escreveu:A definição de progressão aritmética é que a diferença entre dois termos consecutivos é constante. Seguindo isso, tomei dois termos consecutivos e calculei sua diferença, que se mostrou constante. Portanto é uma progressão aritmética.

Muitíssimo obrigada^^

ma bolinha de tênis, após se chocar com o solo, no ponto O, segue uma trajetória ao longo de quatro parábolas. A altura máxima atingida em cada uma das parábolas é 4/3 do valor da altura máxima da parábola anterior. Sabendo-se que as distâncias entre os pontos onde a bolinha toca o solo são iguais ...

(UFRGS) Considere esta progressão geométrica: 3 ; 0,3 ; 0,03 ; 0,003 ; ... Os logaritmos decimais de cada um destes números, na ordem em que estão dispostos Nós já temos uma progressão geométrica dada por 3 \cdot 10^{-n} . Ele quer que consideremos os logaritmos decimais , logo devemos tomar b_n = ...

Se o lado do quadrado é L_n = \frac{1}{2^{\frac{n}{2}}} , então sua área será (L_n)^2 = \left( \frac{1}{2^{\frac{n}{2}}} \right)^2 = \frac{1}{2^n} . Logo terá uma nova progressão geométrica infinita 1, \frac{1}{2}, \frac{1}{2^2}, \frac{1}{2^3}, \ldots . Agora a razão será \frac{1}{2...

Existe um erro na minha resolução, simplifiquei errado. A conta correta é 2(7-a)-a = 14 -3a = \sqrt{a^2 + (7-a)^2} . Resolvendo isto você encontrará a=3 , daí b=4 e a \cdot b = 12 . Como você encontrou a equação 7x^2 -70x +147=0 ? Eu simplifiquei diferente: \sqrt[]{{x}^{2}+{(7-x...

(UFRGS) Considere esta progressão geométrica: 3 ; 0,3 ; 0,03 ; 0,003 ; ... Os logaritmos decimais de cada um destes números, na ordem em que estão dispostos, formam uma: a) progressão geométrica de razão 0,01. b) progressão geométrica de razão 0,1; c) progressão aritmética de razão 0,1. d) progressã...

Considerando uma infinidade de quadrados de lados medindo 1, \frac{1}{\sqrt[]{2}},\frac{1}{\sqrt[]{{2}^{2}}}, \frac{1}{\sqrt[]{{2}^{3}}}..... em cm, é correto afirmar que a soma das áreas de todos esses quadrados é, em cm², igual a a)1/4 b)1/2 c)4 d)2 Eu percebi que é soma de PG infinita, mas não co...

Ju , boa tarde! \\ 50000 < \frac{3(1 - 2^n)}{1 - 2} < 100000 \\\\\\ 50000 < \frac{3(1 - 2^n)}{- 1} < 100000 \\\\ 50000 < - 3(1 - 2^n) < 100000 \\ 50000 < 3(- 1 + 2^n) < 100000 \\\\ \textup{Para que essa divisão seja exata, devemos fazer} \\\\ 49998 < 3(- 1 + 2^n&...

Uma bolinha de tênis, após se chocar com o solo, no ponto O, segue uma trajetória ao longo de quatro parábolas. A altura máxima atingida em cada uma das parábolas é 4/3 do valor da altura máxima da parábola anterior. Sabendo-se que as distâncias entre os pontos onde a bolinha toca o solo são iguais ...

young_jedi escreveu:correto, é isso ai mesmo!!

Mto obrigada mesmo pela assistência =D

a_1.(a_1.q).(a_1.q^2)=1 como são multiplicações eu posso escrever assimm a_1.a_1.a_1.q.q^2=2 apenas alterei a ordem do fatores o produto continua sendo o mesmo a_1^3.q^3=1 tambem posso colocar o expoente em evidencia (a_1.q)^3=1 tirando a raiz cubica da dos dois lados da equ...

a_1.(a_1q).(a_1q^2)=1 a_1^3.q^3=1 a_1.q=1 a_1=\frac{1}{q} na outra equação a_1+q_1q+a_1q^2=\frac{21}{4} substituindo os valores encontrados \frac{1}{q}+1+1.q=\frac{21}{4} tente resolver esta equação para encontrar q e comente as duvidas Não entendi pq de a_1.(a_1q).(a_1q...

Tentem ser o mais claro possível, por favor. Obg. Exigente, né?! :-O Dica: \\ 50000 < S_n < 100000 \\\\\\ 50000 < \frac{a_1(1 - q^n)}{1 - q} < 100000 50000<\frac{3(1-{2}^{n})}{1-2}<100000 50000<\frac{3+3.(-{2}^{n})}{-1}<100000 -50000<3+3.(-{2}^{n})<-100000 -50003<3.&...

Uma progressão geométrica crescente é formada por três termos positivos cujo produto é 1. Determine essa PG, sabendo que a soma dos três termos é 21/4. Ok. Então: a1.(a1.q).(a1.{q}^{2})=1 a1+(a1.q)+(a1.{q}^{2})=\frac{21}{4} Mas não sei como se desenvolve essa conta. M...

Sejam a e b os lados do retângulo e d sua diagonal. Como é um retângulo, podemos aplicar o teorema de pitágoras para encontrar que d = \sqrt{a^2 +b^2} . Pela definição de perímetro temos que 2a + 2b = 14 ou a+b=7 . Pela definição de progressão aritmética sabemos que a razão entre dois termos consec...

Para que a soma dos n primeiros termos da progressão geométrica 3,6,12,24,..... seja um número compreendido entre 50000 e 100000, deveremos tomar n igual a?
Me ajudem, eu não sei como se faz isso. Já vi outras resoluções mas não compreendi. Tentem ser o mais claro possível, por favor. Obg.

\\ \begin{cases} a_2 - a_1 = 9 \\ a_5 - a_4 = 576 \end{cases} \\\\\\ \begin{cases} a_1 \cdot q - a_1 = 9 \\ a_4 \cdot q - a_4 = 576 \end{cases} \\\\\\ \begin{cases} a_1(q - 1) = 9 \Rightarrow (q - 1) = \frac{9}{a_1} \\\\ a_4(q - 1) = 576 \Rightarrow (q - 1) = \frac{5...

Numa progressão geométrica a diferença entre o 2º e o 1º termos é 9 e a diferença entre o 5º e o 4º termos é 576. O primeiro termo da progressão é?
Eu sei o raciocínio, o problema é que não sei fazer as contas. Me ajudem?

As medidas dos lados de um retângulo e sua diagonal formam, nessa ordem, uma PA. Sabendo=se que o perímetro desse retângulo é igual a 14, determine a área desse retângulo.
Questão muito simples mas não sei fazer uma conta com os lados e diagonais formando uma PA. Me ajudem?

UFLA-MG Um prédio de 51 andares, um apartamento por andar, a partir do segundo andar, foi construído de tal forma que o interfone de cada apartamento é ligado por um fio exclusivo ao interfone da portaria, situada no primeiro andar. A altura do prédio é de 153 metros. Desconsidere a quantidade de fi...

Gostaria de saber se minha resolução está correta.
${({log}_{2}x)}^{2}-2{log}_{2}x-8\geq0$
${k}^{2}-2k-8\geq0$
$k={log}_{2}x$
$x={2}^{k}$
Se k = 4, então:
$x={2}^{4}$

E se k = -2, então:
$x={2}^{k}$
$x={2}^{-2}$
$x=\frac{1}{4}$
Está correto?
Estou muito confusa =s

Estar correta sim . Perceba que 3x^2 - 11 > 0 , somando 11 ambos lados vamos obter 3 x^2 > 11 , multiplicando por 1/3 segue que x^2 > 11/3 e finalmente elevando ambos lados a 1/2 , (x^2)^{1/2} > (11/3)^{1/2} < |x| que nos leva a \begin{cases} x> \sqrt{11/3} \\ x> - \sqrt{11/3} \end{...

JU201015, o " i " da fórmula é a taxa à qual o capital está sujeito. Na minha opinião, o correto seria deixar a questão para quando você estudar juros compostos.. Enfim, é você quem sabe :y: Qualquer coisa estamos por aqui. Att, Cleyson007 Culpa da minha apostila que tem esses exercicios ...

JU201015, o " i " da fórmula é a taxa à qual o capital está sujeito. Na minha opinião, o correto seria deixar a questão para quando você estudar juros compostos.. Enfim, é você quem sabe :y: Qualquer coisa estamos por aqui. Att, Cleyson007 Culpa da minha apostila que tem esses exercicios ...

Aplique log pela esquerda e direita da igualdade , isto é log(M) = log (C \cdot (1+i)^n) = log(c) + log(1+i)^n = log(c) + n \cdot log(1+i) . Somando - log(C) e mutiplicando ambos lados por 1/log(1+i) segue que , Log(M) ...

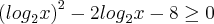
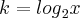
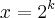
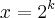
young_jedi escreveu:Certo, é isso ai mesmo!!!

Mto obrigada^^

Me digam se resolvi corretamente? {log}_{4}(3{x}^{2}-11)-{log}_{4}(3x+1)=1 {log}_{4}\frac{3{x}^{2}-11}{3x+1}=1 \frac{3{x}^{2}-11}{3x+1}=4 3{x}^{2}-11=12x+4 3{x}^{2}-12x-15=0 x=5 e x=-1 Condição de existência: 3x+1>0 3x>-1 x>-1/3 Então x = 5 Obs: não consegui fazer a condição de exist...

PUC - SP Um capital C, aplicado a juros compostos a uma taxa unitária i por período, produz,ao final de n períodos, o montante M, dado por M = C.{(1+i)}^{n} . Nessas condições, utilizando-se de log 2=0,30 e log 3=0,48, o capital de R$2000,00, aplicado a juro composto a taxa 20% ao ano, produ...

como cresce expoencialmente então a equação é do tipo f(t)=ab^{kt} como a população dobra a cada vinte minutos dividinto do tempo em minutos temos t/20 f(t)=a.2^{\frac{t}{20}} cmo no inicio (t=0) a população é 1000 então 1000=a.2^{\frac{0}{20}} a=1000 então a função sera f(t)...

Pesquisar

Pesquisa resultou em 54 ocorrências

Re: [Equação quadrática]-UFLA-MG

Re: [Progressão Geométrica e Logaritmo]

Re: [Equação quadrática]-UFLA-MG

Re: [Progressão Geométrica e Logaritmo]

Re: [Progressão Geométrica]

Re: [Progressão Aritmética]

[Progressão Geométrica e Logaritmo]

[Progressão Geométrica]

Re: [Progressão Geométrica]

[Equação quadrática]-UFLA-MG

Re: [Progressão Geométrica]

Re: [Progressão Geométrica]

Re: [Progressão Geométrica]

Re: [Progressão Geométrica]

[Progressão Geométrica]

Re: [Progressão Aritmética]

[Progressão Geométrica]

Re: [Progressão Geométrica]-PUC-SP

[Progressão Geométrica]-PUC-SP

[Progressão Aritmética]

Progressão Aritmética

[Logaritmo]

Re: [Logaritmo]

Re: Logaritmo

Re: Logaritmo

Re: Logaritmo

Re: [Equação exponencial]

[Logaritmo]

Logaritmo

Re: [Equação exponencial]