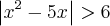
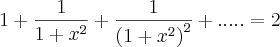Ajuda Matemática • Pesquisar

\\ \log 8 + \log 35 - \log 28 = \\\\ \log 2^3 + \log (7 \cdot 5) - \log (2^3 \cdot 7) = \\\\ \log 2^3 + \log 7 + \log 5 - (\log 2^3 + \log 7) = \\\\ \cancel{\log 2^3} + \cancel{\log 7} + \log 5 \cancel{- \log 2^3} \cancel{- \log 7} = \\\\ \boxed{\log 5} As alternativas -5, 5...

Me ajudem nesse logaritmo?

O que eu faço primeiro? A subtração dos logaritmos ou a soma? E como eu faço?

Me ajudem nesse logaritmo? {log}_{4}x+{log}_{2}x=6 \frac{{log}_{2}x}{{log}_{2}{2}^{2}}+{log}_{2}x= \frac{{log}_{2}x}{2}+{log}_{2}x=6 \frac{{log}_{2}x+2{log}_{2}x}{2}=6 {log}_{2}x+{log}_{2}{x}^{2}}=12 {log}_{2}x.{x}^{2}=12 {log}_{2}{x}^{3}=12 {2}^{12}={x}^{3} O que eu fiz de errado? As alternativas s...

N descresce ao passar do tempo , no instante t = 0 teremos N = N_0 = 100.000 \text{átomos} . Após t unidades de tempo , temos que N = 100 . Qual valor que t deve assumir para termos N = 100 , sabendo que N_0 = 100.000 \text{átomos} ? Basta resolver , 100 = 10^5 \cdot 2^{-t} . Aplicando logaritmo no...

Você está confundindo união com interseção . A interseção entre estes dois conjuntos é vazia. Interseção entre dois conjuntos significa todos os elementos que pertencem a cada um simultaneamente, o que de fato não ocorre. A união entre eles não. União entre dois conjuntos significa todos os element...

$\left|{x}^{2}-5x \right|>6$
Eu fiz então:
${x}^{2}-5x+6<0$
E encontrei 2<x<3
E depois:
${x}^{2}-5x-6>0$
E encontrei x<-1 U x>6
A solução final seria união entre estas soluções, mas daria um conjunto vazio. Está errada minha resolução?

Primeiro membro: P.G \\ \begin{cases} a_1 = 1 \\ q = \frac{1}{1 + x^2} \\ S_n = \end{cases} \\\\\\ S_n = \frac{a_1}{1 - q} \Rightarrow S_n = \frac{1}{1 - \frac{1}{1 + x^2}} \Rightarrow S_n = \frac{1}{\frac{x^2}{1 + x^2}} \Rightarrow \boxed{S_n = \frac{1 + x^2}{x^2}} Daí, \\ \frac{1 + x^2}{x^2} = 2 ...

Na equação $1+\frac{1}{1+{x}^{2}}+\frac{1}{{(1+{x}^{2})}^{2}}+.....=2$ , o 1º membro é a soma dos termos de uma progressão geométrica infinita. A soma das raízes da equação é?
Não sei como se faz. Alguém me ajuda?

OK. no problem ! Através da mudança de base , ficamos com , log_2 (x-1 ) - \frac{log_2(2x +6)}{2} . Multiplicando o denominador e numerador por 2 , não estamos alterando o resultado estamos multiplicando por 1 . Veja como fica , \left( log_2 (x-1 ) - \frac{log_2(2x +...

Schoolgirl+t , E se você encontrar a soma total e depois diminuir 50kg e 340kg. Vê se dá certo! A soma de uma P.A é dada por S_n = \frac{(a_1 + a_n)r}{2} Foi a primeira coisa que tentei kk Foi aí que percebi que se ele retira do depósito, então toda a PA é modificada porque a razão será som...

Devemos determinar a solução para x tal que log_2 (x-1) - log_4 (2x + 6) \leq 0 . log_2 (x-1) - log_4 (2x + 6) = log_2 (x-1) - \frac{ log_2 (2x+6) }{ log_2 (4 ) } = \frac{ 2 \cdot log_2 (x-1) - log_2 (2x +6 ) }{2} = \frac{1}{2}...

Um fazendeiro armazenou sua produção de café, no ano de 2004, da seguinte maneira: Janeiro ......... .100kg Fevereiro.........110kg Março ............120kg e assim, sucessivamente, no decorrer de 12 meses ininterruptamente. Sabe-se que ele retirou de seu depósito 50kg de café no 7º mês e 340kg, no 1...

Estar quase certo , você cometeu um erro assumindo que o logaritmando é menor ou igual a zero , isto não é verdade .O que é verdade que o logaritmo neste contexto é menor ou igual a zero . Diante disso você deve analisar o intervalo para o logaritmando para a qual uma função função logarítmica é me...

Basta decompor em fatores primos , 81 = 3 \cdot 27 = 3 \cdot 3 \cdot 9 = 3 \cdot 3 \cdot 3 \cdot 3 = 3^4 e 32 = 2 \cdot 16 = 2 \cdot 2^4 = 2^5 . Terá que fazer a mudança de base também . Poxa, eu não sei mesmo como se faz, então não dava pra fazer mais detalhado, sei lah, de um jeito que eu possa e...

Em uma substância radioativa, o número N de átomos de um isótopo de um certo elemento é reduzido à metade após um período de 5000 anos. Ou seja, se t representa o tempo medido em unidades de 5000 anos, e No corresponde ao número de átomos desse isótopo no instante t=0, então N={N}_{0}.{2}^{-1} . Se ...

danjr5 escreveu:Sim!
Mas, tem um detalhe, o denominador não pode ter $x = - \frac{2}{3}$ . Pois, seria IMPOSSÍVEL, enfim o denominador seria ZERO.

O correto seria $S = \left \{ x \in \mathbb{R} / x < - \frac{2}{3} \,\, \cup \,\, x \geq - \frac{5}{14} \right \}$

Ops, me esqueci deste detalhe. Mto obrigada^^

Uma inequação fracionária não pode ser resolvida dessa forma. Deve-se levar em consideração o denominador , também. Tentarei explicar com um simples exemplo, veja: Resolva \frac{x + 8}{x - 2} > - 1 - Inicialmente, devemos fazer com que depois do símbolo de maior (ou qualquer outro) seja zero, ou se...

Queria saber se minha resolução está correta. {log}_{0,3}(x+5)-{log}_{0,3}5\geq{log}_{0,3}(3x+2) {log}_{0,3}\frac{(x+5)}{5}\geq{log}_{0,3}(3x+2) {log}_{0,3}\frac{(x+5)}{5}.\frac{1}{(3x+2)}\geq0 {log}_{0,3}\frac{(x+5}{15x+10}\geq0 \frac{x+5}{15x+10}...

Este exercício é conveniente fazer log_2(x) = p , assim teremos uma equação segundo grau : p^2 - 3p - 4 = 0 . Depois para achar x , basta lembra da definição de logaritmo , se log_2(x) = p então , x = 2^{p} . Neste caso não temos restrição para p , pois para quais valores que p assu...

${({log}_{2}x)}^{2}-{3log}_{2}x-4=0$
Não sei como se resolve. Bom, eu sei que quando está subtraindo, dividimos os logaritmos. Não sei se assim nesse caso. Me ajudem?

SchoolGirl+T, no segundo lado da igualdade você não pode resolver daquela forma (lá é multiplicação de mesma base)! Vou te dar a dica! Passe o 4^(3x+5) da última igualdade dividindo pelo da segunda igualdade. Agora, resolva a primeira igualdade com a terceira. Deu para entender? Qualquer coisa é só...

A população de uma colonia de bactéria E.coli dobra a cada 20 mim . Em um experimento, colocou-se inicialmente em um tubo de ensaio uma amostra com 1000 bactérias por mililitro. No final do experimento obteve-se um total de 4,096.{10}^{6} bactérias por mililitro. Assim sendo o tempo do experimento f...

{8}^{a{x}^{2}+bx+c}={4}^{3x+5}={4}^{3x+5}.{2}^{5{x}^{2}-x-8} a+b+c= ? Eu tentei assim: {2}^{3a{x}^{2}+3b+3c}={2}^{6x+10}={2}^{6x+10}.{2}^{5{x}^{2}-x-8} 3a{x}^{2}+3b+3c=6x+10=6x+10}+5{x}^{2}-x-8 Mas eu não sei fazer esse tipo de equação então, me digam se eu resolvi correto até aqui e como se encont...

considerando que a base é maior que 1 voce encontrou que x<2 portanto 1<x<2 agora considerando que a base é menor que 1 voce encontrou que x>2 mais repare que isto é impossivel pois não tem como um numero x ser maior que 2 e menor que 1 ao mesmo tempo logo a opção acima é a correta. letra d) Obriga...

Supondo x um número real, ( x>0 e x\neq1 ), a inequação {x}^{2x-1}<{x}^{3} tem como solução a) 0<x<3 b) x<1 c) x>2 d) 1<x<2 Bom, eles disseram que x<0, mas, quando igualamos as bases, para mantermos o sinal de inequação ou inverter, precisamos saber se a base é maior ou menor que 1. Nesse caso, a ba...

MarceloFantini escreveu:Se então . Agora você precisa saber que a função com qualquer é sempre positiva, portanto devemos ter ou .

Thanks! ^^

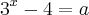A equaçãoi ${3}^{x}-4 = a$ , com "a" real, só terá solução real para
a) a> -4
b) a< 4
c) a> -3
d) a< 3
Eu não sei como fazer isso =( Alguém ajuda?

\\ \left ( 2^x + 2^{- x} \right )^3 = \\\\ \left ( 2^x + \frac{1}{2^x} \right )^3 = \\\\\\ \left ( \frac{2^x \cdot 2^x + 1}{2^x} \right )^3 = \\\\\\ \left ( \frac{2^{2x} + 1}{2^x} \right )^3 = \\\\\\ \left [ \frac{(2^{2x})^3 \cdot (1)^0 + 3 \cdot (...

Como fazer:
${({2}^{x} + {2}^{-x})}^{3}$

Dica , multiplique os dois lados da igualdade por 3^x . Com isso faça 3^x = k , resolva para k , depois volte e resolva para x . Mas lembre -se 3^x > 0 com isso k > 0 . Vale lembrar a propriedade a^b \cdot a^c = a^{b + c} . Ah! Achei "x=2" mas, olha só. Depois que eu resolvi a equação k² ...

Pesquisar

Pesquisa resultou em 57 ocorrências

Re: [Logaritmo]

[Logaritmo]

[Logaritmo]

Re: [Logaritmo]-UFLA-MG

Re: [Inequação quadrática]

[Inequação quadrática]

Re: [Equação]-FGV-SP

[Equação]-FGV-SP

Re: [Logaritmo]

Re: [Progressão Aritmética] SASI/UFVJM-MG

Re: [Logaritmo]

[Progressão Aritmética] SASI/UFVJM-MG

Re: [Logaritmo]

Re: [Logaritmos]

[Logaritmo]-UFLA-MG

Re: [Logaritmo]

Re: [Logaritmo]

[Logaritmo]

Re: [Logaritmo]

[Logaritmo]

Re: [Equação]

[Equação exponencial]

[Equação]

Re: [Equação exponencial]

[Equação exponencial]

Re: [Equação]

[Equação]

Re: [Potenciação]

[Potenciação]

Re: [Função Exponencial] UFJF - MG