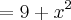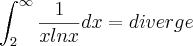
![\int_{2}^{\infty}\frac{1}{\sqrt[]{x}lnx}dx= diverge \int_{2}^{\infty}\frac{1}{\sqrt[]{x}lnx}dx= diverge](/latexrender/pictures/208e99fafe668a52b00195c1534ecac9.png)


![\int_{0}^{\infty}\frac{1}{\sqrt[]{x(x+4)}}dx = \frac{\Pi}{2} \int_{0}^{\infty}\frac{1}{\sqrt[]{x(x+4)}}dx = \frac{\Pi}{2}](/latexrender/pictures/08beffa07146f008e5c6a581ce05e421.png) , com essa resposta ela converge?
, com essa resposta ela converge? , você colocou um x para fora da raiz quadrada , multiplicando toda raiz , no caso onde foi parar o outro x
, você colocou um x para fora da raiz quadrada , multiplicando toda raiz , no caso onde foi parar o outro x , dentro da raiz quando passa multiplicando , me parece que ta faltando um x?
, dentro da raiz quando passa multiplicando , me parece que ta faltando um x?![\lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3 \lim_{x\rightarrow \infty}\frac{\sqrt[]{9x^2+x}}{x+8}=3](/latexrender/pictures/931233037b0ca8ced29c46fa8ae03b95.png)
 estava estudando , e entendi o desenvolvimento , porem no finalzinho onde foi parar o
estava estudando , e entendi o desenvolvimento , porem no finalzinho onde foi parar o 
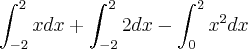
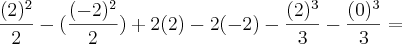
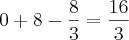
 ou
ou  caso desse uma dessas respostas eu diria que ela diverge , más nao é o caso aqui
caso desse uma dessas respostas eu diria que ela diverge , más nao é o caso aqui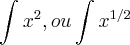
![\sqrt[]{y} \sqrt[]{y}](/latexrender/pictures/2c7054a0a5416b35c805d1e6e3dc1a54.png) e as retas
e as retas

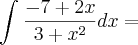
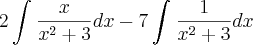
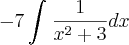
 ) não entendi ! os outros passos entendi.
) não entendi ! os outros passos entendi.

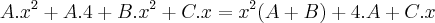
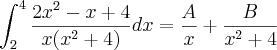
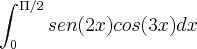
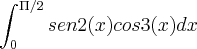
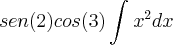 aqui, nao entendi porque sen(2) e cos(3) virarão constantes?
aqui, nao entendi porque sen(2) e cos(3) virarão constantes? eu posso cancelar os dois sinal de menos? por sinal de + !
eu posso cancelar os dois sinal de menos? por sinal de + !
![- \frac{1}{\sqrt[]{(u)}}+c - \frac{1}{\sqrt[]{(u)}}+c](/latexrender/pictures/29f34c96afd6e56f5ff9f1f1c47bb136.png) , agora substituir o valor de (u)
, agora substituir o valor de (u)